ABCD is a quadrilateral in which AB= AD, the bisector of ∠BACand∠CAD intersect the sides BC and CD at the points E and F respectively. Prove that EF || BD.Solution in Tamil
The correct Answer is:=BEEC
Step by step video, text & image solution for ABCD is a quadrilateral in which AB= AD, the bisector of angle BAC and angle CAD intersect the sides BC and CD at the points E and F respectively. Prove that EF || BD. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Similar Questions
ABCD is a quadrilateral in which AB= AD, the bisector of ∠BACand∠CAD intersect the sides BC and CD at the points E and F respectively. Prove that EF || BD.
View SolutionIf ABCD is a quadrilateral and E and F are the midpoints of AC and BD respectively, then prove that −−→AB+−−→AD+−−→CB+−−→CD=4−−→EF.
View Solutionநாற்கரம் ABCD -யில் AB =AD .∠BAC மற்றும் ∠CAD யின் கோணம் இருசமவெட்டிகள் BC ,மற்றும் CD ஆகிய பக்கங்கள் முறையே E மற்றும் F என்ற புள்ளிகள் சந்திக்கிறன்றன .எனில் EF ||BD என் நிறுவுக ?
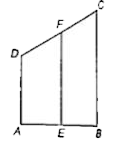
View SolutionABCD is a trapezium , in which AD∣∣BC, E and F are the mid-point of AB and CD respectively , then EF is :
View SolutionABCD is a quadrilateral in which AB=BC and AD=CD ,Show that BD bisects both the ∠ABC and ∠ADC.
View SolutionABCD is a quadrilateral in which AB=AD . The bisector of BAC and CAD intersect the sides BC and CD at the points E and F respectively. Prove that EF||BD.
View Solutionएक चतुर्भुज ABCD में AB =AD है| ∠BAC और ∠CAD के समद्विभाजक, चतुर्भुज की भुजाओं BC व CD को क्रमशः बिंदु E व F पर मिलते है|सिद्ध करो की EF∣∣BD
View Solutionएक चतुर्भुज ABCD में, AB=BC,AD और CD के लम्ब समद्विभाजक E पर मिलते हैं, तो सिद्ध करें कि BE,∠ABC का समद्विभाजक है ।
View Solution