ABCD is a square. A is joined to a point P on BC and D is joined to a point Q on AB. If AP = DQ, prove that AP and DQ are perpendicular to each other.
Step by step video solution for ABCD is a square. A is joined to a point P on BC and D is joined to a point Q on AB. If AP = DQ, prove that AP and DQ are perpendicular to each other. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RECTILINEAR FIGURESBook:ICSEChapter:RECTILINEAR FIGURESExercise:POLYGONS - 3 MARKS QUESTIONS
Explore 5 Videos
- RECTILINEAR FIGURESBook:ICSEChapter:RECTILINEAR FIGURESExercise:POLYGONS - 4 MARKS QUESTIONS
Explore 4 Videos
- RECTILINEAR FIGURESBook:ICSEChapter:RECTILINEAR FIGURESExercise:Exercise 14(B)
Explore 16 Videos
- RATIONAL AND IRRATIONAL NUMBERS Book:ICSEChapter:RATIONAL AND IRRATIONAL NUMBERS Exercise:EXERCISE 1 (D)
Explore 21 Videos
- SIMULTANEOUS EQUATIONSBook:ICSEChapter:SIMULTANEOUS EQUATIONSExercise:EXERCISE 6 (G)
Explore 13 Videos
Similar Questions
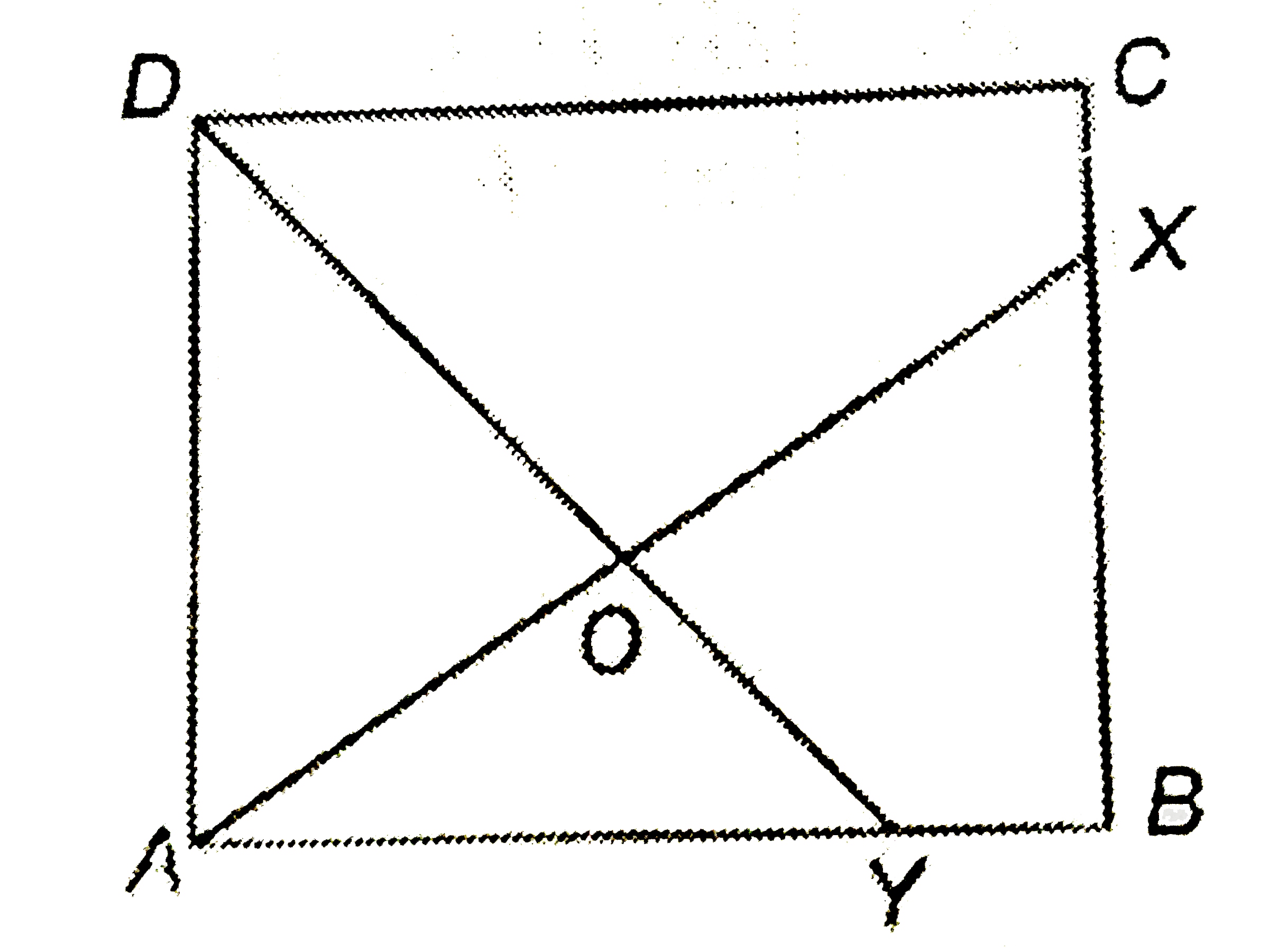
In a square ABCD, A is joined to a point X on BC and D is joined to a point Y on AB. If AX = DY, prove that AX is perpendicular to DY.
View SolutionABCD is a square. P, Q and Rare the points on AB, BC and CD respectively, such that AP = BQ = CR. Prove that:
PQ = QR
View SolutionABCD is a square. P, Q and Rare the points on AB, BC and CD respectively, such that AP = BQ = CR. Prove that:
PB = QC
View SolutionABCD is a square, X is the mid-point of AB and Y the mid-point of BC. Prove that
the triangles ADX and BAY are congruent.
View SolutionIn triangle ABC, the sides AB and AC are equal. If P is a point on AB and Q is a point on AC such that AP = AQ, prove that :
(i) triangle APC and AQB are congruent.
(ii) triangle BPC and CQB are congruent.

View SolutionABCD is a square, X is the mid-point of AB and Y the mid-point of BC. Prove that
DX is perpendicular to AY.
View SolutionIf AP bisects angle BAC and M is any point on AP, prove that the perpendiculars drawn from M to AB and AC are equal.
View SolutionABCD is a square, X is the mid-point of AB and Y the mid-point of BC. Prove that
∠DXA=∠AYB
View SolutionABCD is a parallelogram E is mid-point of AB and DE bisects angle D. Prove that
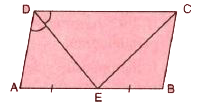
BC= BE
View SolutionIn quadrilateral ABCD, AB=DC and AD=BC. Prove that the sides AB and DC are parallel to each other.
View Solution