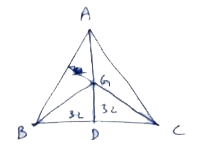
AD is a median of triangle ABC. G is a mid point of AD. If area of triangle ABC is 16 sq. cm. Find the area of triangle GDC

Step by step video solution for AD is a median of triangle ABC. G is a mid point of AD. If area of triangle ABC is 16 sq. cm. Find the area of triangle GDC by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - EXERCISE ( Integer/Numerical Value Type )
5 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Olympiad/HOTS Corner
14 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - EXERCISE ( Subjective Problems ) (Short Answer Type )
4 Videos
- CIRCLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - CIRCLES EXERCISE - OLYMPIAD/HOTS CORNER
6 Videos
Similar Questions
In parallelogram ABCD, AB = 10 cm. The altitudes corresponding to the sides AB and AD are respectively 7 cm and 8 cm. If AD is k cm. Then value of 4 k is
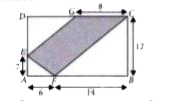
View SolutionIn the given figure ABCD is a rectangle and all measurements are in centimeters. Find the area of the shaded region.
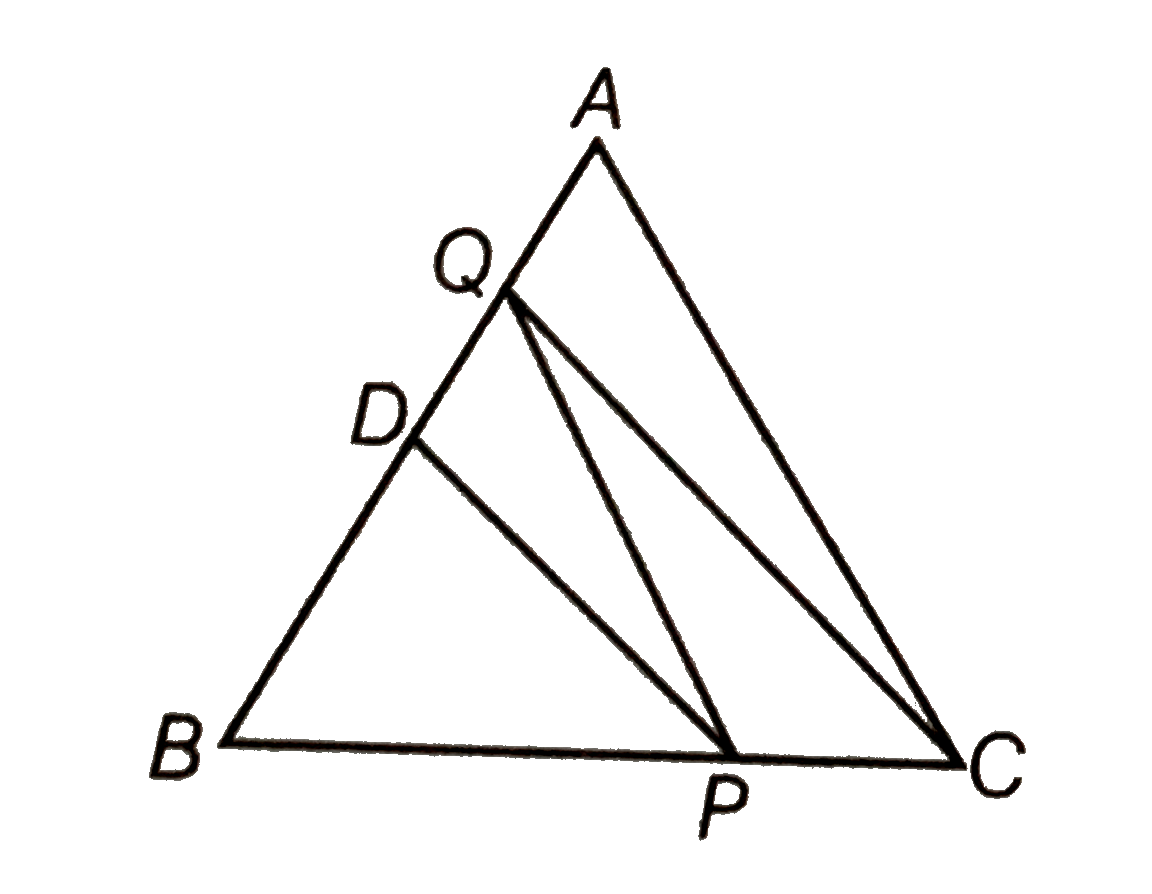
View SolutionIn Δ ABC, D is the mid-point of AB and P is any point on BC. If CQ∣∣PD meets AB and Q (shown in figure), then prove that
ar(ΔBPQ)=12ar(ΔABC).
View SolutionABCD is a cyclic quadrilateral, if ∠BAC=60∘,∠BCA=20∘, then find the value of ∠ADC.
View SolutionIn a triangle ABC,having AD is median and area of triangle ABD=120m^(2). Find area of triangle ABC.
View SolutionIn a ΔABC, medians ADandBE are drawn. If AD=4,∠DAB=π6and∠ABE=π3 then the area of ΔABC is
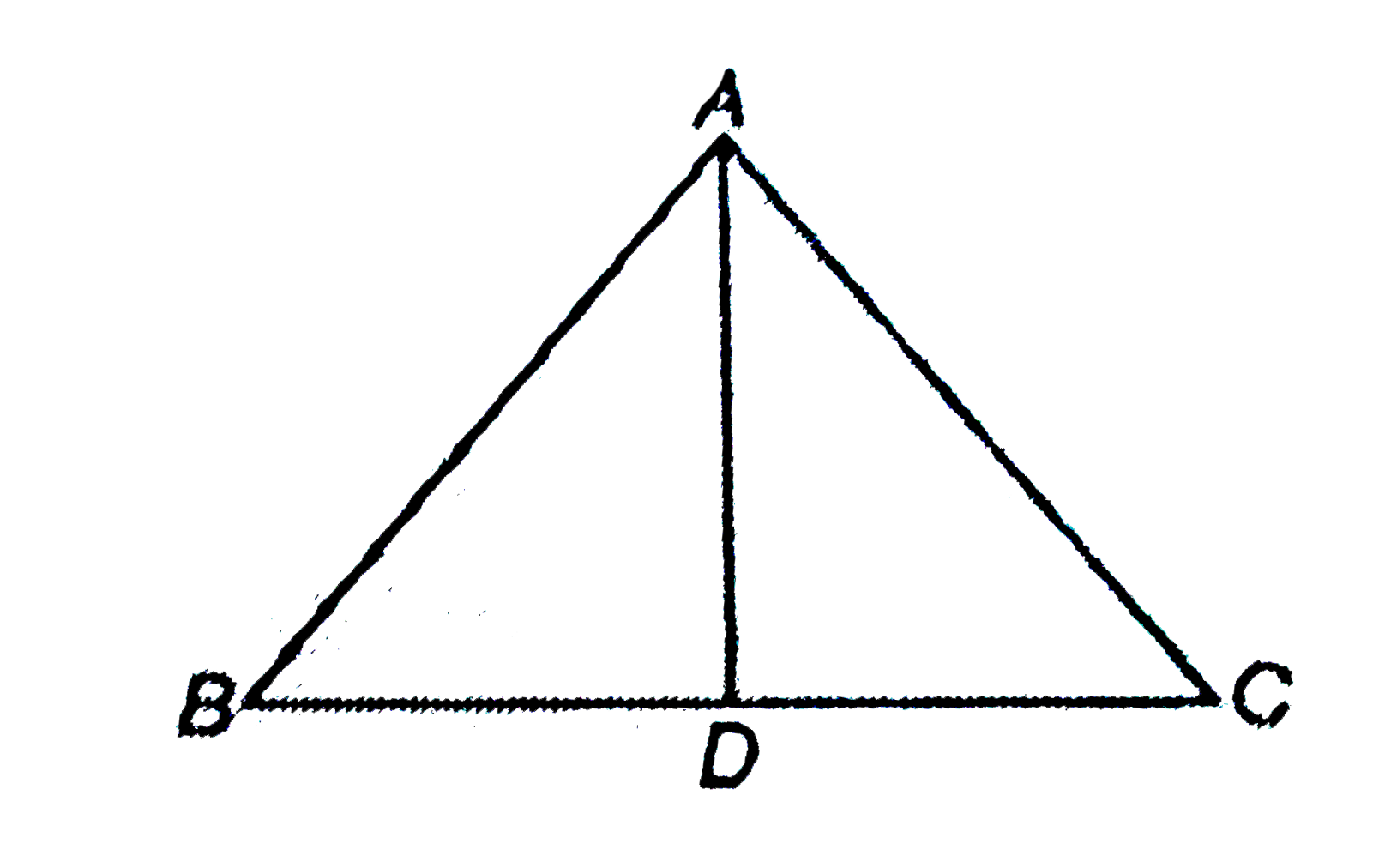
View SolutionIn the given figure AD is the median. If the area of ΔABD=10cm2, find the area of ΔABC
View Solutionयदि त्रिभुज ABC की AD एक माध्यिका है, तो सिद्ध करो कि त्रिभुज ADB और त्रिभुज ADC का क्षेत्रफल बराबर है । यदि माध्यिका AD का मध्य बिंदु G हो, तो सिद्ध करो कि
ar(ΔBGC)=2ar(ΔAGC) है।
View Solutionसमबाहु त्रिभुज ABC की AD एक ऊंचाई है|यदि AD को आधार लेकर एक समबाहु त्रिभुज ADE बनाई गई है तो सिद्ध करो की Area(ΔADE):Area(ΔABC)=3:4
View Solution(ix) AD, BE and CF are the three medians of ΔABC and intersect at G. The area of the ΔABC is 36 Sq. cm. Find (a) the area of ΔAGB and (b) the area of the quadrilateral BDGF.
View SolutionP is a point on the median AD of the ΔABC. Prove that area of ΔAPB = area of ΔAPC.
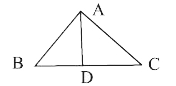
View SolutionIn ΔABC,AD is median. If area of ΔABD=25cm2 find the area of ΔABC.
View SolutionΔ ABC की तीन माध्यिकाएं AD, BE और CF एक दूसरे को G पर काटती हैं। यदि ABC का क्षेत्रफल 36 वर्ग सेमी हो, तो Δ CGE का क्षेत्रफल है-
View SolutionIn a ΔABC, G is centroid and AD, BE, CF are medians. Find the area of quadrilateral BDGF, if the area of ΔABC=72cm2
View SolutionAD is a median of triangle ABC. G is a mid point of AD. If area of triangle ABC is 16 sq. cm. Find the area of triangle GDC
View SolutionIn a ΔABC,AD is median, G is a Mid point of AD. If area of ΔAGC IS 32 SQ . units then find area of ΔBGC
View Solution
