AD is an altitude of an isosceles ΔABC in which AB = AC.
Show that (i) AD bisects BC,
(ii) AD bisects ∠A.
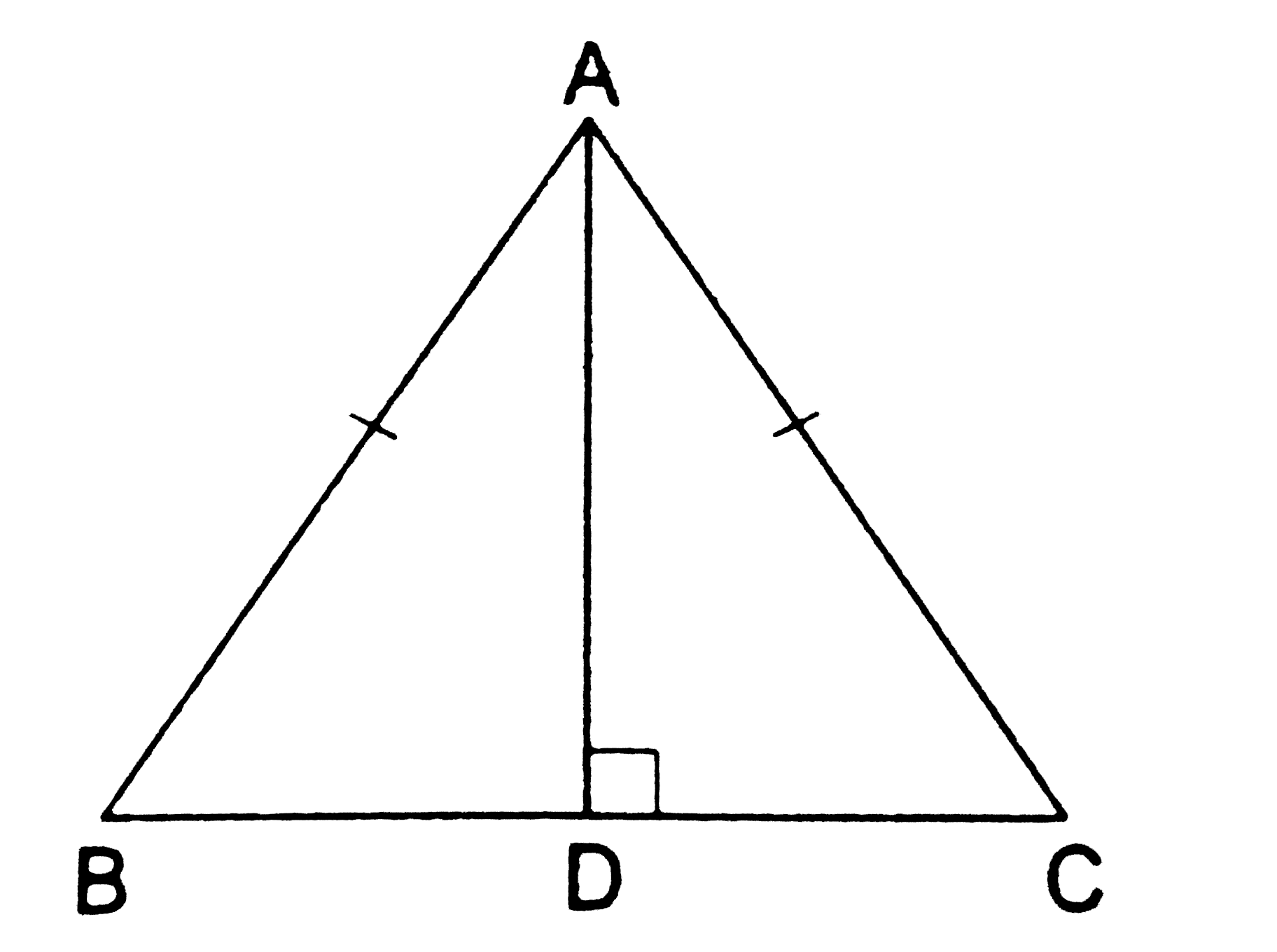
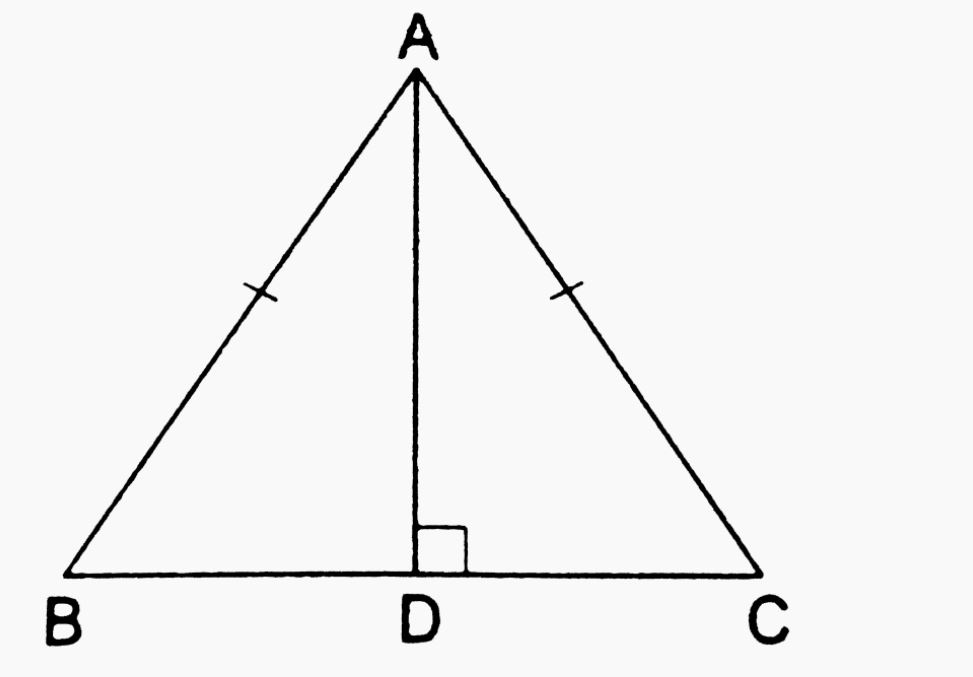
(i) In ΔBAD and ΔCAD,
∠ADB=∠ADC (Each 90∘as AD is an altitude)
AB=AC (Given)
AD=AD (Common)
∴ ΔBAD≅ΔCAD (By RHS Congruence rule)
∴ BD=CD (By CPCT)
Hence, AD bisects BC.
(ii) Since,ΔBAD≅ΔCAD
By CPCT, ∠BAD=∠CAD
Hence, AD bisects ∠A.
Similar Questions
AD एक समद्विबाहु त्रिभुज ABC का एक सिर्शलम्ब है, जिसमे AB=AC है दर्शाइए की (i) AD रेखाखण्ड BC को समद्विभाजित करता है, (ii) AD कोण A को समद्विभाजित करता है
View Solutionएक समद्विबाहु त्रिभुज में यदि AB=AC है और A से भुजा BC पर एक शीर्षलम्ब AD है, तो सिध्द करो कि
(i)∠B=∠C
(ii)AD,BC को समद्विभाजित करता है |
(iii)AD,∠Aको समद्विभाजित करता है |
View SolutionAD is an altiude of an isosceles triangle ABC in which AB = AC. Show that
(i) AD bisects BC (ii) AD bisects A.
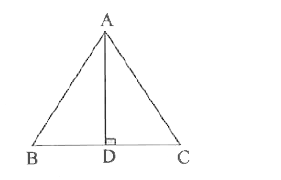
View SolutionAD is an altitude of an isosceles triangle ABC in which AB = AC. Show that, (i) AD bisects BC (ii) AD bisects ∠A.
View SolutionAD is an altitude of an isosceles triangle ABC in which AB = AC. Show that, (i) AD bisects BC (ii) AD bisects ∠A.
View SolutionAD is an altitude of an isosceles triangle ABC in which AB = AC. Show that, (i) AD bisects BC (ii) AD bisects ∠A.
View SolutionAD is an altitude of an isosceles triangle ABC in which AB = AC. Show that, (i) AD bisects BC (ii) AD bisects ∠A.
View SolutionAD एक समद्धिबाहू त्रिहुज ABC का एक शीर्षलम्ब है, जिसमे AB -= AC है | दर्शाइए कि
(i) AD रेखाखण्ड BC को समद्धिभाजित करता है |
(ii) AD कोण A को समद्धिभाजित करता है |
View Solution
