AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that:- AD bisects BCSolution in Punjabi
Step by step video solution for AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that:- AD bisects BC by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLES Book:SWAN PUBLICATIONChapter:TRIANGLES Exercise:EXERCISE 7.4
Explore 6 Videos
- TRIANGLES Book:SWAN PUBLICATIONChapter:TRIANGLES Exercise:EXERCISE 7.5
Explore 4 Videos
- TRIANGLES Book:SWAN PUBLICATIONChapter:TRIANGLES Exercise:EXERCISE 7.2
Explore 10 Videos
- SURFACE AREAS AND VOLUMES Book:SWAN PUBLICATIONChapter:SURFACE AREAS AND VOLUMES Exercise:Objective Type Questions (Fill in the Blanks )
Explore 7 Videos
Similar Questions
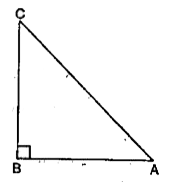
Show that in a right angled triangle, the hypotenuse is the longest side.
View SolutionABC is a triangle. Locate a point in the interior of ΔABC which is equidistant from all the vertices of ΔABC.
View SolutionIn an isosclees triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at O. Join A to O show that : OB=OC.
View SolutionTotal surface area of a cone = ..............
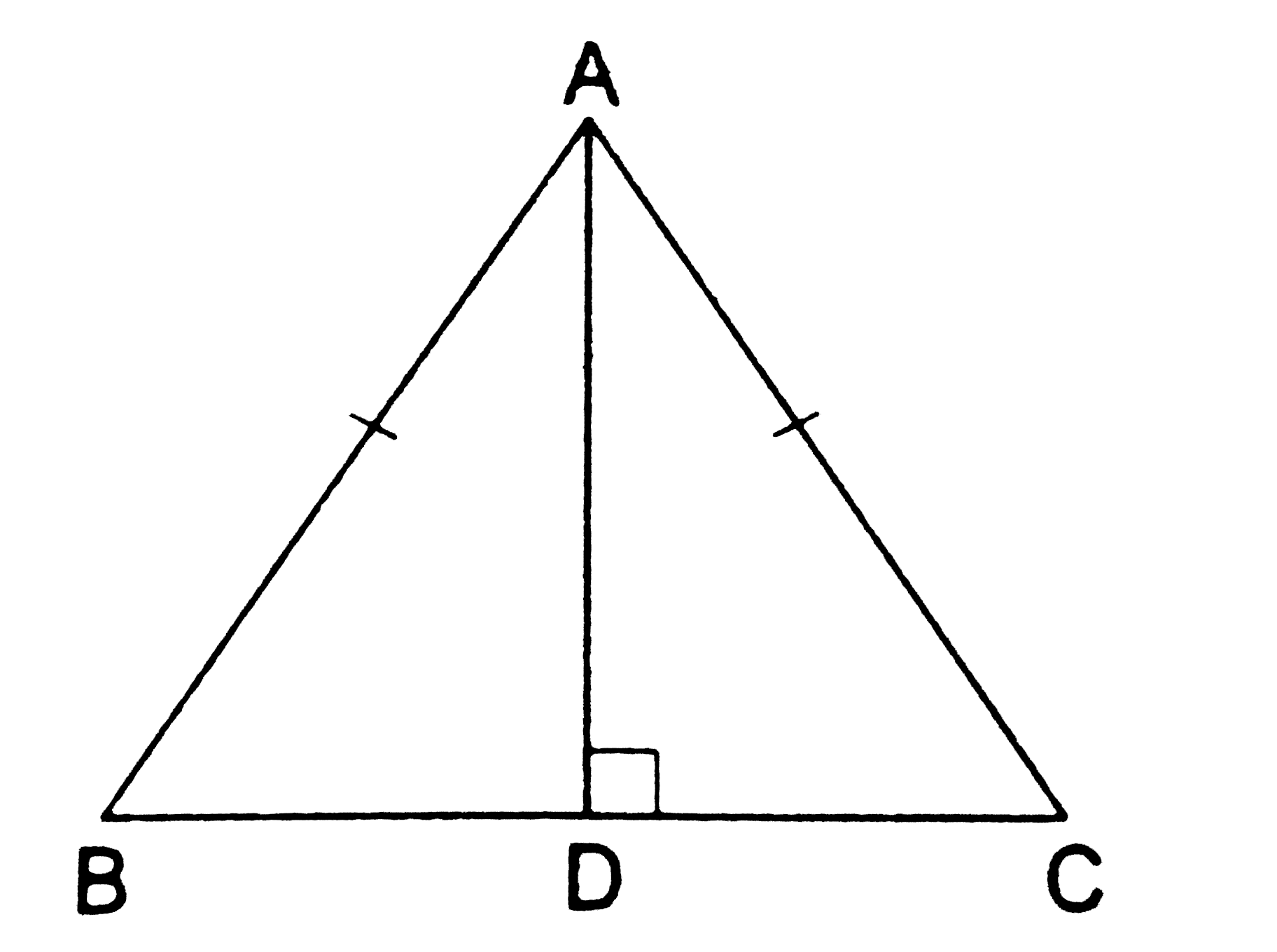
View SolutionIf ΔABC is an isosceles triangle such that AB=AC, then altitude AD from A on BC bisects BC (Fig.43).
View SolutionAD is an altitude of an isosceles ΔABC in which AB = AC.
Show that (i) AD bisects BC,
(ii) AD bisects ∠A.
View SolutionAD एक समद्विबाहु त्रिभुज ABC का एक शीर्षलम्ब है, जिसमें AB = AC है। दर्शाइए कि
(i) AD रेखाखंड BC को समद्विभाजित करता है। (ii ) AD कोण A को समद्विभाजित करता है।
View SolutionAD एक समद्विबाहु त्रिभुज ABC का एक सिर्शलम्ब है, जिसमे AB=AC है दर्शाइए की (i) AD रेखाखण्ड BC को समद्विभाजित करता है, (ii) AD कोण A को समद्विभाजित करता है
View SolutionAD is an altiude of an isosceles triangle ABC in which AB = AC. Show that
(i) AD bisects BC (ii) AD bisects A.
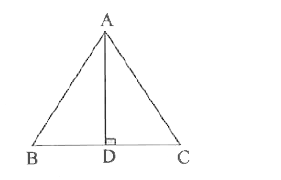
View SolutionAD is an altitude of an isosceles triangle ABC in which AB = AC. Show that, (i) AD bisects BC (ii) AD bisects ∠A.
View SolutionAD is an altitude of an isosceles triangle ABC in which AB = AC. Show that, (i) AD bisects BC (ii) AD bisects ∠A.
View SolutionAD is an altitude of an isosceles triangle ABC in which AB = AC. Show that, (i) AD bisects BC (ii) AD bisects ∠A.
View SolutionAD is an altitude of an isosceles triangle ABC in which AB = AC. Show that, (i) AD bisects BC (ii) AD bisects ∠A.
View SolutionAD एक समद्धिबाहू त्रिहुज ABC का एक शीर्षलम्ब है, जिसमे AB -= AC है | दर्शाइए कि
(i) AD रेखाखण्ड BC को समद्धिभाजित करता है |
(ii) AD कोण A को समद्धिभाजित करता है |
View SolutionAD is an altitude of an isosceles ΔABC in which AB = AC.
Show that (i) AD bisects BC,
(ii) AD bisects ∠A.

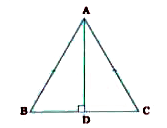
View SolutionAD is an altitude of an isosceles triangle ABC in which AB = AC. Show that: ( i ) AD bisects BC ( ii) AD bisects ∠ A
View Solution