As we know studied that a median of a triangle divides it into triangles of equal areas. Verify this result for ΔABC whose vertices are A (4,-6), B(3,-2) and C (5,2).
The correct Answer is:3 sq. units
To verify that the median of triangle ABC divides it into two triangles of equal area, we will follow these steps:
Step 1: Identify the vertices of the triangle
The vertices of triangle ABC are given as:
- A (4, -6)
- B (3, -2)
- C (5, 2)
Step 2: Find the midpoint D of side BC
To find the midpoint D of side BC, we use the midpoint formula:
D(x1+x22,y1+y22)
where B(3,−2) and C(5,2).
Calculating the coordinates of D:
D(3+52,−2+22)=D(82,02)=D(4,0)
Step 3: Calculate the area of triangle ABD
We will use the formula for the area of a triangle given by vertices (x1,y1), (x2,y2), and (x3,y3):
Area=12|x1(y2−y3)+x2(y3−y1)+x3(y1−y2)|
For triangle ABD, the vertices are:
- A(4, -6)
- B(3, -2)
- D(4, 0)
Substituting the coordinates into the area formula:
AreaABD=12|4(−2−0)+3(0+6)+4(−6+2)|
Calculating this:
=12|4(−2)+3(6)+4(−4)|
=12|−8+18−16|
=12|−6|=62=3
Step 4: Calculate the area of triangle ADC
For triangle ADC, the vertices are:
- A(4, -6)
- D(4, 0)
- C(5, 2)
Using the area formula again:
AreaADC=12|4(0−2)+4(2+6)+5(−6−0)|
Calculating this:
=12|4(−2)+4(8)+5(−6)|
=12|−8+32−30|
=12|−6|=62=3
Step 5: Compare the areas
We have found that:
- Area of triangle ABD = 3
- Area of triangle ADC = 3
Since both areas are equal, we have verified that the median AD divides triangle ABC into two triangles of equal area.
Conclusion
Thus, we can conclude that the median of a triangle divides it into two triangles of equal area. Hence proved.
---
The vertices of triangle ABC are given as:
- A (4, -6)
- B (3, -2)
- C (5, 2)
To find the midpoint D of side BC, we use the midpoint formula:
D(x1+x22,y1+y22)
where B(3,−2) and C(5,2).
D(3+52,−2+22)=D(82,02)=D(4,0)
We will use the formula for the area of a triangle given by vertices (x1,y1), (x2,y2), and (x3,y3):
Area=12|x1(y2−y3)+x2(y3−y1)+x3(y1−y2)|
For triangle ABD, the vertices are:
- A(4, -6)
- B(3, -2)
- D(4, 0)
AreaABD=12|4(−2−0)+3(0+6)+4(−6+2)|
Calculating this:
=12|4(−2)+3(6)+4(−4)|
=12|−8+18−16|
=12|−6|=62=3
For triangle ADC, the vertices are:
- A(4, -6)
- D(4, 0)
- C(5, 2)
AreaADC=12|4(0−2)+4(2+6)+5(−6−0)|
Calculating this:
=12|4(−2)+4(8)+5(−6)|
=12|−8+32−30|
=12|−6|=62=3
We have found that:
- Area of triangle ABD = 3
- Area of triangle ADC = 3
Thus, we can conclude that the median of a triangle divides it into two triangles of equal area. Hence proved.
Topper's Solved these Questions
- LINES (IN TWO - DIMENSIONS)BOOK - OSWAL PUBLICATIONCHAPTER - LINES (IN TWO - DIMENSIONS)EXERCISE - NCERT CORNER (TEXTBOOK QUESTIONS) (EXERCISE - 7.4)
13 Videos
- LINES (IN TWO - DIMENSIONS)BOOK - OSWAL PUBLICATIONCHAPTER - LINES (IN TWO - DIMENSIONS)EXERCISE - NCERT EXEMPLAR (EXERCISE - 7.1)
20 Videos
- LINES (IN TWO - DIMENSIONS)BOOK - OSWAL PUBLICATIONCHAPTER - LINES (IN TWO - DIMENSIONS)EXERCISE - NCERT CORNER (TEXTBOOK QUESTIONS) (EXERCISE - 7.2)
10 Videos
- INTRODUCTION TO TRIGONOMETRY AND TRIGONOMETRIC IDENTITIES BOOK - OSWAL PUBLICATIONCHAPTER - INTRODUCTION TO TRIGONOMETRY AND TRIGONOMETRIC IDENTITIES EXERCISE - BOARD CORNER (Long Solution Type Questions)
6 Videos
- LINES (IN TWO DIMENSIONS) BOOK - OSWAL PUBLICATIONCHAPTER - LINES (IN TWO DIMENSIONS) EXERCISE - CASE - BASED MCQs
15 Videos
Similar Questions
Determine the ratio in which the line 2x +y 4 = 0 divides the line segment joining the points A(2, 2) and B(3,7).
View SolutionThe distance of the point P (2,3) from the Y-axis is
View SolutionFind the coordinates of the point which divides the join of A(−1,7) and B(4,−3) in the ratio 2:3.
View SolutionProve that sinA−cosA+1sinA+cosA−1=1secA−tanA
View SolutionRead the following text and answer the following questions on the basis of the same :
Class X students of a secondary school in Krishnagar have been allotted a rectangular plot of a land for gardening activity. Saplings of Gulmohar are planted on the boundary at distance of 1 m from each other in the fig. The students are to sow seeds of flowering plants on the remaining area of the plot.
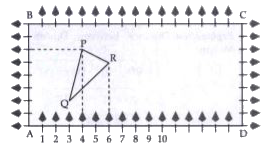
What are the coordinates of A ?
View SolutionYou have studied in Class IX, (Chapter 9. Example 3), that a median of a triangle divides it into two triangles of equal areas. Verify this result for ∆ ABC whose vertices A(4, – 6), B(3, –2) and C(5, 2).
View SolutionIf A(4,−6),B(3,−2)andC(5,2) are the vertices of ABC, then verify the fact that a median of a triangle ABC divides it into two triangles of equal areas.
View SolutionIf A (1,2) , B(-2, 3) and C(-3,-4) be the vertices of ΔABC . Verify that median BE divides it into two triangles of equal areas.
View Solutionकक्षा IX में आपने पढ़ा है (अध्याय 9, उदाहरण 3) कि किसी त्रिभुज की एक माधियका उसे बराबर क्षेत्रफलों वाले दो त्रिभुजों में विभाजित करती है | उस त्रिभुज ABC के लिए इस परिणाम का सत्यापन कीजिए जिसके शीर्ष A(4,−6),B(3,−2) और C(5,2) हैं |
View SolutionA(7, -3), B(5, 3) and C(3, -1) are the vertices of a ΔABC and AD is its median. Prove that the median AD divides ΔABC into two triangles of equal areas.
View Solutionआप जानते है कि किसी त्रिभुज कि एक माधियका उसे बराबर क्षेत्रफलों वालो दो त्रिभुजों में विभाजित करती है। उस त्रिभुज ABC के लिए इस परिणाम का सत्यापन कीजिये जिसके शीर्ष A(4,−6),B(3,−2) और C(5,2) है।
View Solutionत्रिभुज कि मध्यिका त्रिभुज के क्षेत्रफल को दो समान भागो में बाटती है | इस कथन को ΔABC के लिए सत्यापित करे जिसके शीर्ष A(4,−6),B(3,−2) और C≡(5,2) है |
View Solutionयदि ΔABC के शीर्ष A(4,−6),B(3,−2) और C(5,2) हैं तो इस तथ्य को सत्यापित कीजिए कि त्रिभुज ABC की माध्यिका इसे दो बराबर क्षेत्रफलों वाले त्रिभुजों में विभाजित करती है ।
View Solutionयदि A(4, -6), B(3, -2) और C(5, 2) एक त्रिभुज ABC के शीर्ष तथा AD इसकी माध्यिका है, तो सिध्द कीजिए कि माध्यिका AD, ΔABC को बराबर क्षेत्रफल के दो त्रिभुजों में विभाजित करती है ।
View Solutionकक्षा IX में आपने पढ़ा है की किसी त्रिभुज की एक मध्यिका उसे बराबर क्षेत्रफलों वाले दो त्रिभुजों में विभाजित करती है । उस त्रिभुज ABC के लिए इस परिणाम का सत्यापन कीजिए जिसके शीर्ष A(4, -6), B(3, -2) और C(5, 2) हैं ।
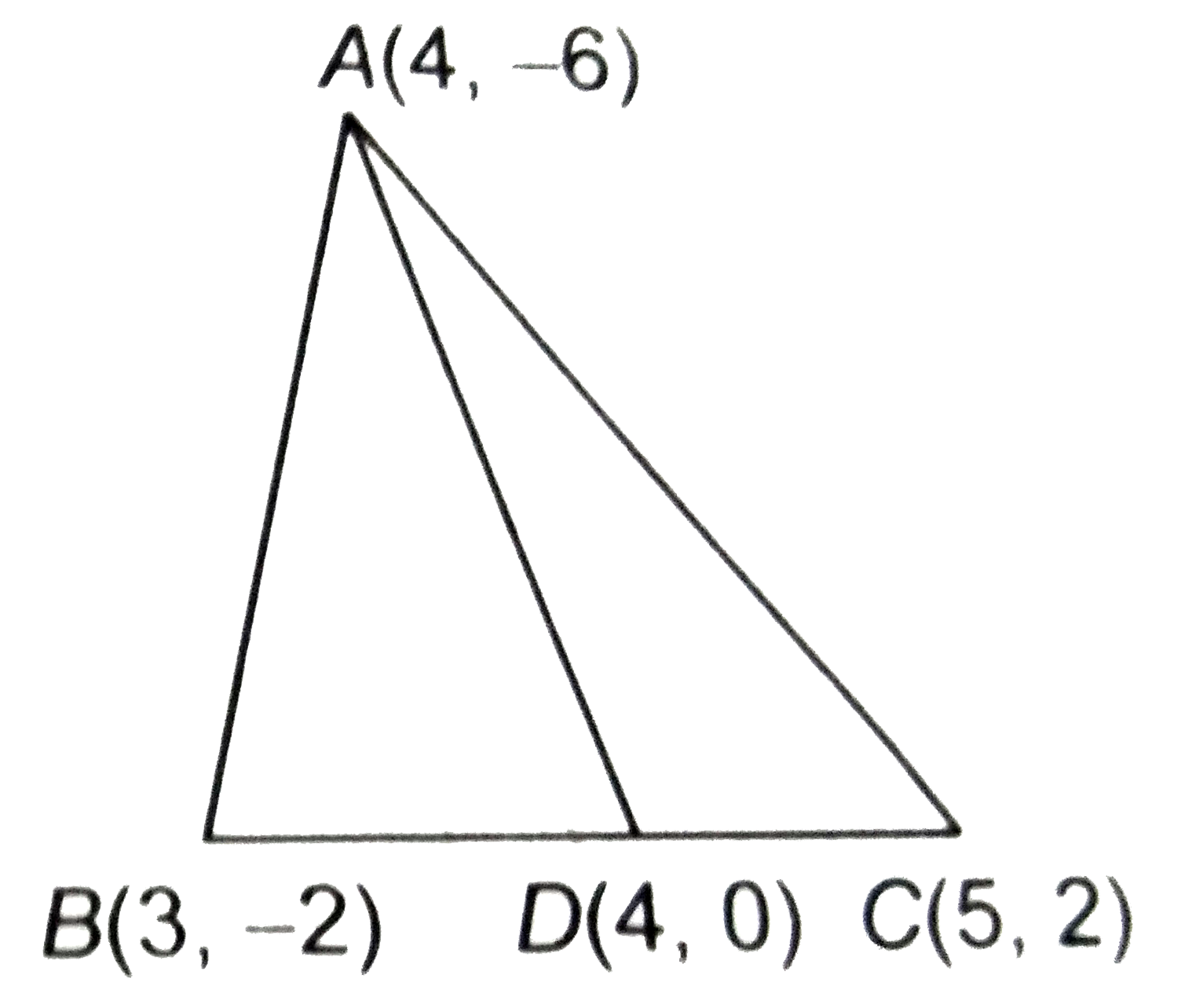
View SolutionYou have studied in Class IX, (Chapter 9, Example 3), that a median of a triangle divides it into two triangles of equal areas. Verify this result for ΔABC whose vertices are A(4, -6), B(3, -2) and C(5, 2).
View Solution
