Calculate the mean deviation about the median of the following observation: 3011,2780,3020,2354,3541,4150,5000
To calculate the mean deviation about the median for the given observations, we will follow these steps:
Step 1: Arrange the data in ascending order.
The given observations are:
3011, 2780, 3020, 2354, 3541, 4150, 5000.
Arranging them in ascending order:
2354, 2780, 3011, 3020, 3541, 4150, 5000.
Step 2: Find the median.
Since there are 7 observations (an odd number), the median is the middle value.
The median is the 4th observation in the ordered list:
Median = 3020.
Step 3: Calculate the absolute deviations from the median.
We will calculate the absolute difference between each observation and the median (3020).
1. |2354 - 3020| = 666
2. |2780 - 3020| = 240
3. |3011 - 3020| = 9
4. |3020 - 3020| = 0
5. |3541 - 3020| = 521
6. |4150 - 3020| = 1130
7. |5000 - 3020| = 1980
Step 4: Sum the absolute deviations.
Now, we will sum all the absolute deviations calculated in the previous step:
Total = 666 + 240 + 9 + 0 + 521 + 1130 + 1980 = 4546.
Step 5: Calculate the mean deviation.
The mean deviation is calculated by dividing the total absolute deviation by the number of observations.
Mean Deviation = Total Absolute Deviation / Number of Observations
Mean Deviation = 4546 / 7 = 649.42.
Final Answer:
The mean deviation about the median of the given observations is 649.42.
---
The given observations are:
3011, 2780, 3020, 2354, 3541, 4150, 5000.
2354, 2780, 3011, 3020, 3541, 4150, 5000.
Since there are 7 observations (an odd number), the median is the middle value.
Median = 3020.
We will calculate the absolute difference between each observation and the median (3020).
2. |2780 - 3020| = 240
3. |3011 - 3020| = 9
4. |3020 - 3020| = 0
5. |3541 - 3020| = 521
6. |4150 - 3020| = 1130
7. |5000 - 3020| = 1980
Now, we will sum all the absolute deviations calculated in the previous step:
Total = 666 + 240 + 9 + 0 + 521 + 1130 + 1980 = 4546.
The mean deviation is calculated by dividing the total absolute deviation by the number of observations.
Mean Deviation = 4546 / 7 = 649.42.
The mean deviation about the median of the given observations is 649.42.
Topper's Solved these Questions
Similar Questions
Calculate the mean deviation about the median of the following observation: 38,70,48,34,63,42,55,44,53,47
View SolutionCalculate the mean deviation about the median of the following observation:22,24,30,27,29,31,25,28,41,42
View SolutionFind the mean deviation about the mean for the following data :

View SolutionFind the mean deviation about the mean for the following data :

View SolutionFind the mean deviation about the mean for the following data :

View SolutionFind the mean deviation about median for the following data:

View SolutionFind the mean deviation about the mean for the following data.

View SolutionFind the mean deviation about mean for the following data:

View SolutionFind the mean deviation from the median for the following data:
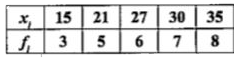
View SolutionFind the mean deviation about the median for the following data:4,6,9,3,10,13,2
View Solution
