Check whether the following shapes are symmetrical or not.

The correct Answer is:Symmetric
Step by step video solution for Check whether the following shapes are symmetrical or not. by Maths experts to help you in doubts & scoring excellent marks in Class 6 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SYMMETRYBook:MTG IIT JEE FOUNDATIONChapter:SYMMETRYExercise:Exercise (Subjective Problems) Long Answer Type
Explore 1 Video
- SYMMETRYBook:MTG IIT JEE FOUNDATIONChapter:SYMMETRYExercise:Exercise (Integer/Numerical Value Type)
Explore 5 Videos
- SYMMETRYBook:MTG IIT JEE FOUNDATIONChapter:SYMMETRYExercise:Exercise (Subjective Problems) Very Short Answer Type
Explore 14 Videos
- RATIO AND PROPORTIONBook:MTG IIT JEE FOUNDATIONChapter:RATIO AND PROPORTIONExercise:OLYMPAID/HOTS CORNER
Explore 15 Videos
- UNDERSTANDING ELEMENTARY SHAPES Book:MTG IIT JEE FOUNDATIONChapter:UNDERSTANDING ELEMENTARY SHAPES Exercise:OLYMPIAD/HOTS CORNER
Explore 20 Videos
Similar Questions
Check whether the following figures are symmetric or not. If yes, draw the line of symmetry in each of the following.

View SolutionCheck whether the following figures are symmetric or not. If yes, draw the line of symmetry in each of the following.

View SolutionCheck whether the following figures are symmetric or not. If yes, draw the line of symmetry in each of the following.
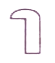
View SolutionCheck whether the following figures are symmetric or not. If yes, draw the line of symmetry in each of the following.

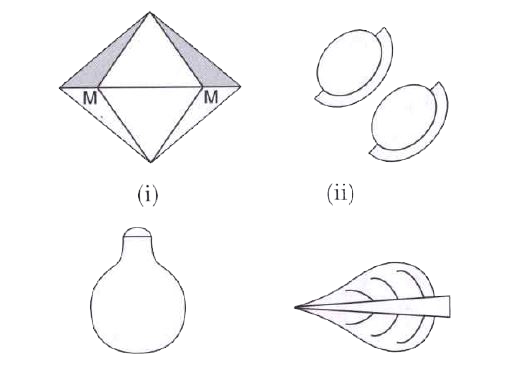
View SolutionCheck which of the following figures are symmetrical.
View SolutionCheck whether the following are perfect squares or not :
(a) 64x2+81y2−144xy
(b) 4x2+8y2+16xy
View SolutionCheck whether the following are perfect squares or not :
(a) 64x2+81y2−144xy
(b) 4x2+8y2+16xy
View SolutionCheck whether the followings represent function or not (i) x2+y2=36,y∈[0,6]
View SolutionCheck whether the following are in proportion or not :
(i) 2,4,6,8 (ii) 12, 18, 10 ,15
View SolutionCheck whether the following sentence is a statement. Give reasons for your answer: Every set is a finite set.
View Solution