Complete the hexagonal and star shaped Rangolies [see Fig. 7.53 (i) and (ii)] by filling them with as many equilateral triangles of side 1 cm as you can. Count the number of triangles in each case. Which has more triangles?
![Complete the hexagonal and star shaped Rangolies [see Fig. 7.53 (i) and (ii)] by filling them with as many equilateral triangles of side 1 cm as you can. Count the number of triangles in each case. Which has more triangles?](https://d10lpgp6xz60nq.cloudfront.net/physics_images/IX_HIN_MATH_C07_E05_004_Q01.png)
(##IX07_E0504_s01##)
Let's find the area of ΔOAB
Area of an equilateral triangle of side 'a' is given by √34a2
Area of ΔOAB=√34(side)2
=√34(5cm)2
=25√34cm2
Area of hexagonal-shaped rangoli = 6×25√34cm2=75√32cm2
Area of an equilateral triangle of side1cm=√34(1cm)2=√34cm2
Number of equilateral triangles of 1 cm side that can be filled in this hexagonal-shaped Rangoli = Area of hexagonal-shaped rangoli / Area of an equilateral triangle of side 1 cm
⇒75√32√34=150
Star-shaped rangoli has 12 equilateral triangles of side 5 cm in it.
Topper's Solved these Questions
Similar Questions
In each of the following, state if the statement is true (T) or false (F): (i) A triangle has three sides. (ii) A triangle may have four vertices. (iii) Any three line-segments make up a triangle. (iv) The interior of a triangle includes its vertices. (v) The triangular region includes the vertices of the corresponding triangle. (vi) The vertices of a triangle are three collinear points. (vii) An equilateral triangle is isosceles also. (viii) Every right triangle is scalene. (ix) Each acute triangle is equilateral. (x) No isosceles triangle is obtuse.
View SolutionA uniform conducting wire of length 12a and resistance R is wound up as a current carrying coil in the shape of (i) an equilateral triangle of side a, (ii) a square of sides a and, (iii) a regular hexagon of sides a. The coil is connected to a voltage source V0. Find the magnetic moment of the coils in each case.
View SolutionSome identical balls are arranged in rows to form an equilateral triangle. The first row consists of one ball, the second row consists of row balls and so on. If 99 more identical balls are added to the total number of balls used in forming the equilateral triangle, then all these balls can be arranged in a square whose each side contains exactly 2 balls less than the number of balls each side of the triangle contains. Then, the number of balls used to form the equilateral triangle is
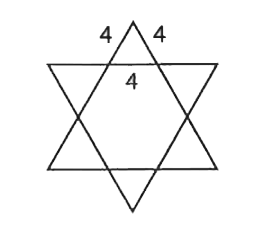
View SolutionThe point of a six-pointed star consist of six identical equilateral triangles, with each side 4 cm (see figure). What is the area of the entire star, including the center?
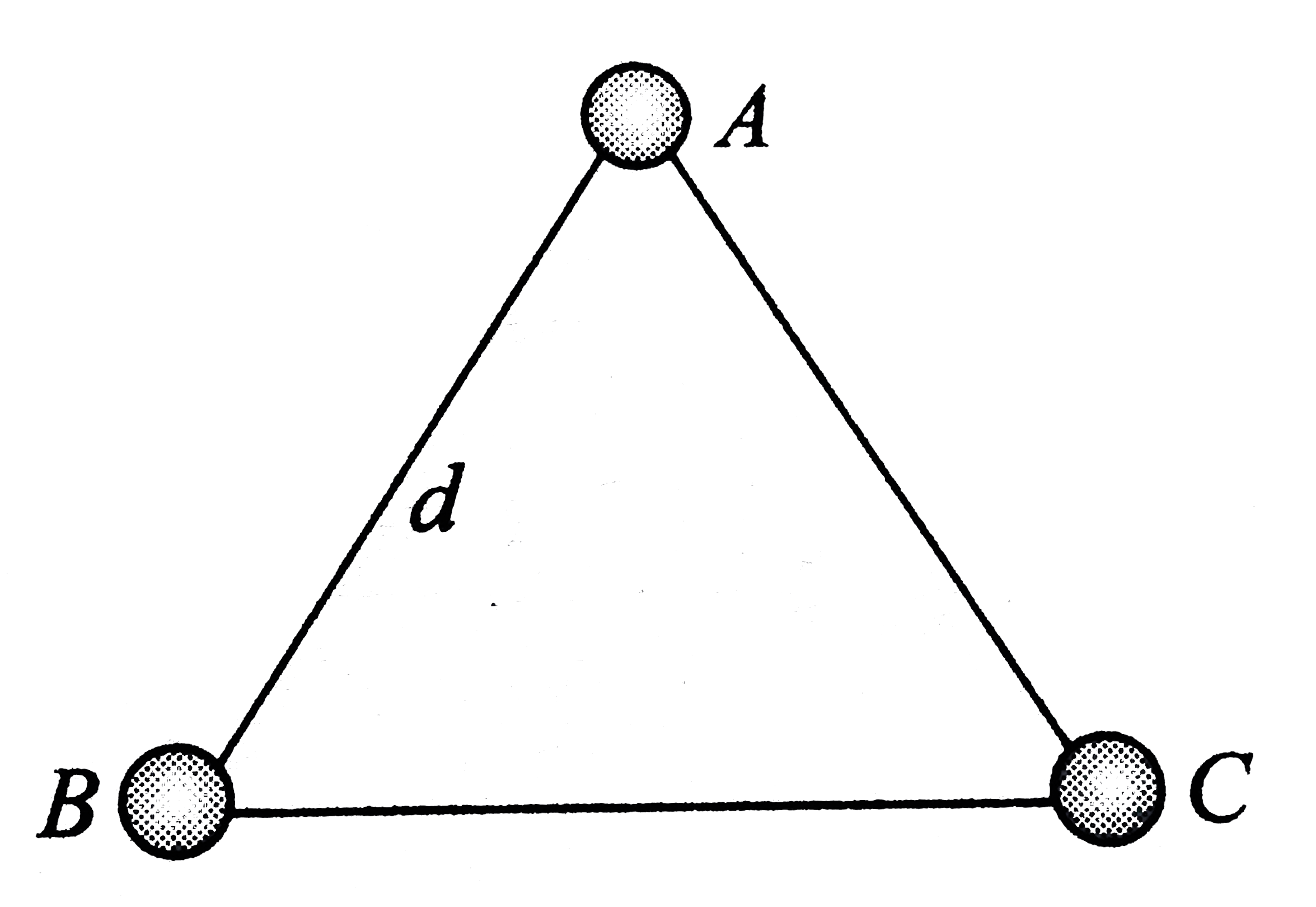
View SolutionThree identical metallic uncheged spheres A,B,andC, each of radius a, are kept at the corners of an equilateral triangle of side d(d>>a) as shown in (Fig. 3.137). The fourth sphere (of radius a), which has a charge q, touches A and is then removed a position far away. B is earthed and then the earth connection is removed. C is then earthed. The charge on C is
 .
.
View SolutionOn a squared paper, draw (i) a rectangle, (ii) a triangle (iii) any irregular closed figure. Find the approximate area of each by counting the number of squares complete, more than half and exactly half.
View SolutionFill in the blanks with correct word/symbol to make it a true statement: (i) A triangle has .. sides. (ii) A triangle has ..vertices. (iii) A triangle has ..angles. (iv) A triangle has ..parts. (v) A triangle whose no two side are equal is known as.. (vi) A triangle whose two sides are equal is known as (vii) A triangle whose all the sides are equal is known as (viii) A triangle whose one angle is a right angle is known as. (ix) A triangle whose all the angles are of measure less than 900 is known as (x) A triangle whose one angle is more than 900 is known as.....
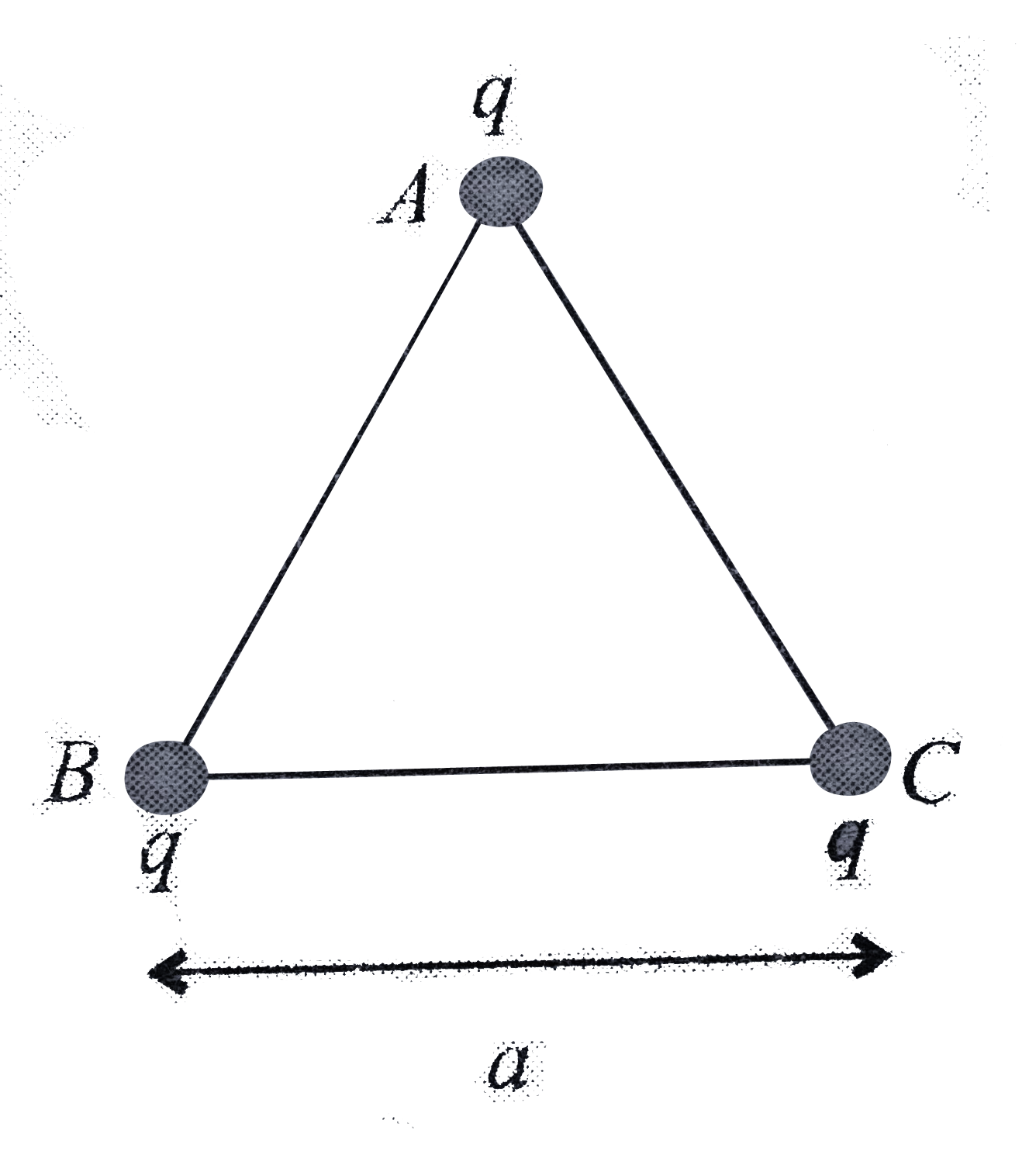
View SolutionThree equal charges q are placed at the corners of an equilateral triangle of side A.
(i) Find out potential energy of charge system.
(ii) Calculate work required to decrease the side of triangle to a/2.
(iii) If the charges are released from the shown position and each of them has same mass m, then find the speed of each particle when they lie on triangle of side 2a.
 .
.
View SolutionThree equal charges q are placed at the corners of an equilateral triangle of side A.
(i) Find out potential energy of charge system.
(ii) Calculate work required to decrease the side of triangle to a/2.
(iii) If the charges are released from the shown position and each of them has same mass m, then find the speed of each particle when they lie on triangle of side 2a.
 .
.
View SolutionEach of two parallel lines has a number of distinct points marked on them. On one line there are 2 points P and Q and on the other there are 8 points. i. Find the number of triangles formed having three of the 10 points as vertices. ii. How many of these triangles include P but exclude Q?
View Solution
