Condition identitiy : If a+b+c=0 then a3+b3+c3=3abc
abc
3abc
2abc
-3abc
The correct Answer is:B
Step by step video & text solution for Condition identitiy : If a+b+c=0 then a^3 + b^3+c^3 = 3abc by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- POLYNOMIALSBook:MTG IIT JEE FOUNDATIONChapter:POLYNOMIALSExercise:EXERCISE (Multiple choice Question (Level2))
Explore 15 Videos
- POLYNOMIALSBook:MTG IIT JEE FOUNDATIONChapter:POLYNOMIALSExercise:EXERCISE (Match the following)
Explore 3 Videos
- POLYNOMIALSBook:MTG IIT JEE FOUNDATIONChapter:POLYNOMIALSExercise:NCERT Section (Exercise 2.5)
Explore 16 Videos
- NUMBER SYSTEMSBook:MTG IIT JEE FOUNDATIONChapter:NUMBER SYSTEMSExercise:Olympiad/HOTS Corner
Explore 20 Videos
- PROBABILITYBook:MTG IIT JEE FOUNDATIONChapter:PROBABILITYExercise:OLYMPIAD/HOTS CORNER
Explore 20 Videos
Similar Questions
One of the factor of (a+2b)3+(2a−c)3−(a+2c)3+3(a+2b)(2a−c)(a+2c) is
View SolutionList-II shows the degree of polynomials given in List -I.
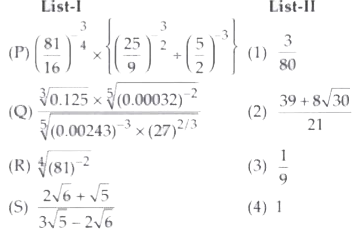
View SolutionUse suitable identities to find the following products :
(i) (x+4)(x+10) (ii)(x+8)(x−10)
(iii)(3x+4)(3x−5) (iv)(y2+32)(y2−32)
(v)(3−2x)(3+2x)
View SolutionWhich of the following statements is incorrect ?
View SolutionA bag contains 8 red and 4_ green balls. One ball is selected at random. Find the probability that the ball drawn is red.
View Solution[[b+c,a-b,ac+a,b-c,ba+b,c-a,c]]=3abc-a^(3)-b^(3)-c^(3)
View SolutionIf a+b+c=0 then prove that a^(3)+b^(3)+c^(3)=3abc
View SolutionCondition identitiy : If a+b+c=0 then a3+b3+c3=3abc
View SolutionIf a13+ b13+ c13=0 then
(a)a+b+c=0 (b) (a+b+c)3=27 abc (c)a+b+c=3abc (d) a3+b3+c3=0
View SolutionIf the roots of the equation (a^(2)-bc)x^(2)+2(b^(2)-ca)x+(c^(2)-ab)=0 are equal then the condition is (i)a+b+c=0(ii)a^(3)+b^(3)+c^(3)-3abc=0 (iii) a=0 or a^(3)+b^(3)+c^(3)-3abc=0 (iv) b=0 or a^(3)+b^(3)+c^(3)-3abc=0
View SolutionProve that |(a+b, b, c), (b+c, c, a), (c+a, a, b)| = 3abc - a^3-b^3-c^3.
View SolutionIf (a-b)=3,(b-c)=5 and (c-a)=1 then the value of (a^(3)+b^(3)+c^(3)-3abc)/(a+b+c) is?
View Solutionसिद्ध कीजिए की ∣∣ ∣∣a+bbcb+ccac+aab∣∣ ∣∣=3abc−a3−b3−c3
View Solutionसिद्ध कीजिए कि: ∣∣ ∣∣a+bbcb+ccac+aab∣∣ ∣∣=3abc−a3−b3−c3.
View Solutionयदि a+b+c=0, तो दिखाइए कि a3+b3+c3=3abc.
View Solution(i) सिद्ध करें की ∣∣ ∣∣a+bbcb+ccac+aab∣∣ ∣∣=3abc−a3−b3−c3
View Solution