Consider the following graph of the function y=f(x). Which of the following is//are correct?
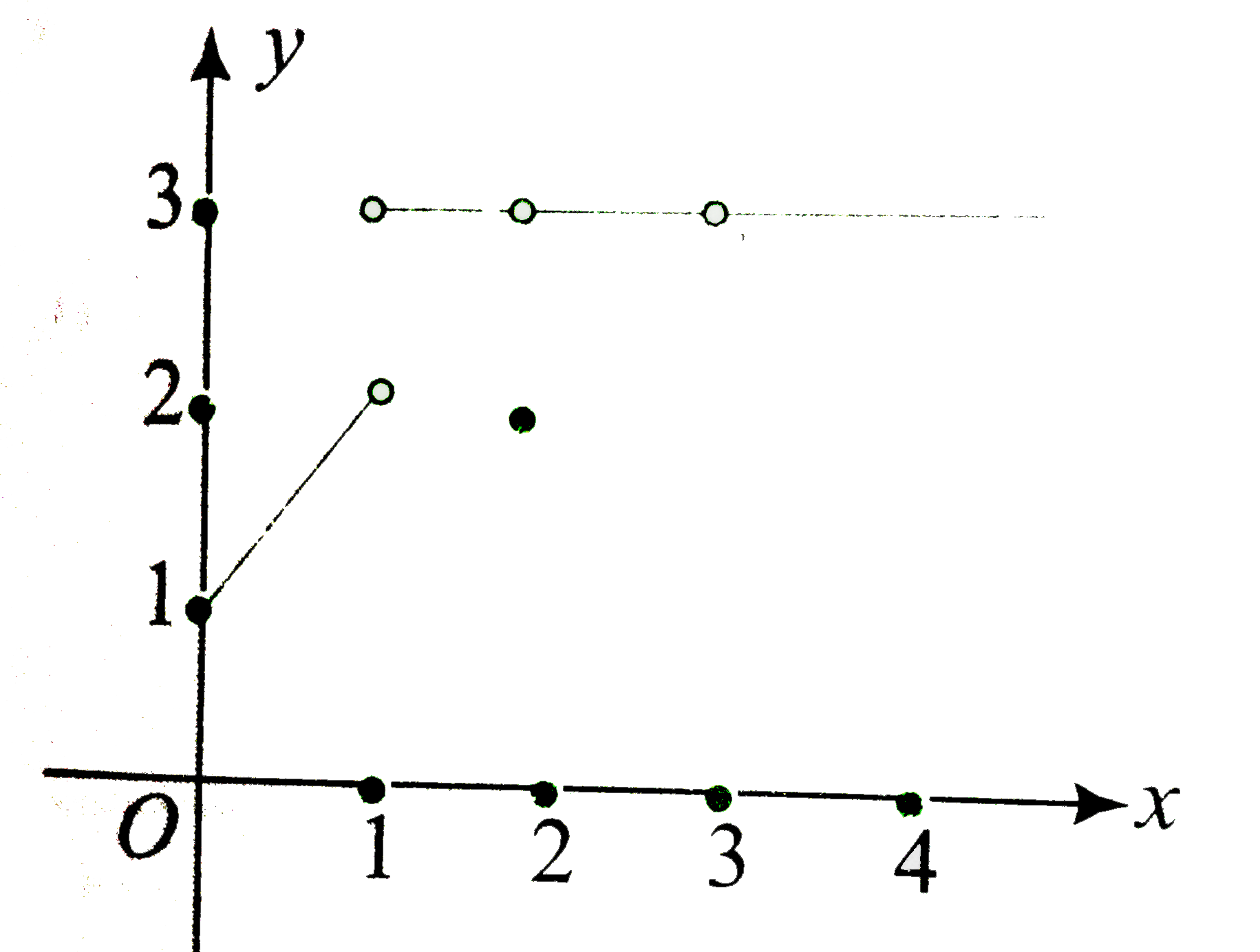
(a)limx→1f(x) does not exist.
(b)limx→2f(x) does not exist.
(c)limx→3f(x)=3.
(d)limx→1.99f(x)exists.Solution in Bengali
The correct Answer is:(a), ( c ), (d)
a.limx→1+f(x)=3 and limx→1−f(x)=2. Thus,limx→1f(x) does not exist.
b.limx→2+f(x)=limx→2−f(x)=3. Thus,limx→2f(x) exist.
c.limx→3+f(x)=limx→3−f(x)=3. Thus,limx→3f(x) exist.
d.limx→1.99+f(x)=limx→1.99−f(x)=3. Thus,limx→1.99f(x) exist.
टॉपर्स ने हल किए ये सवाल
- LIMITSBook:CENGAGE PUBLICATIONChapter:LIMITSExercise:EXERCISE 2.2
Explore 7 Videos
- LIMITSBook:CENGAGE PUBLICATIONChapter:LIMITSExercise:EXERCISE 2.3
Explore 14 Videos
- LIMITSBook:CENGAGE PUBLICATIONChapter:LIMITSExercise:Solved Examples
Explore 15 Videos
- JEE 2019Book:CENGAGE PUBLICATIONChapter:JEE 2019Exercise:Chapter 10
Explore 8 Videos
- LOGARITHM AND ITS PROPERTIESBook:CENGAGE PUBLICATIONChapter:LOGARITHM AND ITS PROPERTIESExercise:JEE ADVANCED
Explore 1 Video
समान प्रश्न
If |f(x)|≤x2, then prove that limx→0f(x)x=0.
View SolutionEvaluate limx→1(2x−3)(√x−1)2x2+x−3.
View SolutionEvaluate:limn→∞n2⎧⎪ ⎪⎨⎪ ⎪⎩ ⎷(1−cos(1n)) ⎷(1−cos(1n))√(1−cos(1n))..∞⎫⎪ ⎪⎬⎪ ⎪⎭.
View SolutionIf y = y(x) is the solution of the differential equation, xdydx+2y=x2 satisfying y(1) = 1, then y(12) is equal to
View SolutionLet (x0,y0) be the solution of the following equations: (2x)1n2=(3y)1n3 31nx=21ny The x0 is 16 (b) 13 (c) 12 (d) 6
View SolutionIf (lim)x→a[f(x)g(x)] exists, then both (lim)x→af(x)and(lim)x→ag(x) exist.
View SolutionWhich of the following statements about the function y=f(x) graphed here are true,an which are false ?( a )lim_(x rarr-1)f(x)=1(b)lim_(x rarr2)f(x) does not exist.
View Solutionlim_(x rarr c)f(x) does not exist when: (A) f(x)=[[x]]-[2x-1],c=3
View SolutionWhich of the following statement(s) is (are) INCORRECT ?. (A) If lim_(x->c) f(x) and lim_(x->c) g(x) both does not exist then lim_(x->c) f(g(x)) also does not exist.(B) If lim_(x->c) f(x) and lim_(x->c) g(x) both does not exist then lim_(x->c) f'(g(x)) also does not exist.(C) If lim_(x->c) f(x) exists and lim_(x->c) g(x) does not exist then lim_(x->c) g(f(x)) does not exist. (D) If lim_(x->c) f(x) and lim_(x->c) g(x) both exist then lim_(x->c) f(g(x)) and lim_(x->c) g(f(x)) also exist.
View SolutionConsider the following graph of the function y=f(x). Which of the following is//are correct?

(a)limx→1f(x) does not exist.
(b)limx→2f(x) does not exist.
(c)limx→3f(x)=3.
(d)limx→1.99f(x)exists.
View SolutionIf f(x)=sgn(x) and g(x)=x3,then prove that limx→0f(x).g(x) exists though limx→0f(x) does not exist.
View Solutionयदि f एक फलां इस प्रकार है कि f(−x)=−f(x) तथा limx→0f(x) का अस्तित्व है तब सिद्ध कीजिए कि limx→0f(x)=0
View SolutionStatement - I: if limx→0(sinxx+f(x)) does not exist, then limx→0f(x) does not exist.
Statement - II: limx→0sinxx=1
View SolutionSketch the graph of a function f that satisfies the given values:
f(-2) = 0 , f(2) = 0 , limx→−2f(x)=0
limx→2f(x) does not exist.
View SolutionConsider the function f(x)=sqrtx,xge0 . Does lim_(xto0)f(x) exist?
View Solutionयदि limx→a[f(x).g(x)] का अस्तित्व है, तब limx→af(x) और limx→ag(x) का अस्तित्व है |
View Solution
