Draw the graph of f(x)=|sinx|+|cosx|,x∈R.
Video Solution
Text Solution
We have y=f(x)=|sinx|+|cosx|,x∈R
Now f(x+π2)=∣∣∣sin(x+π2)∣∣∣+∣∣∣cos(x+π2)∣∣∣
=|cosx|+|−sinx|
=|cosx|+|sinx|
= f(x)
Thus, the period of y=f(x) is π2
We need to draw the graph of the function for x∈[0,π2]
f(x)=sinx+cosx=√2sin(π4+x) for x∈[0,π2]
f(0)=f(π/2)=1,f(π4)=√2sin(π4+π4)=√2
Also f''(x)=sinx−cosx<0 for x∈[0,π2]
Therefore, the graph is concave downwards.
Hence the graph of y=f(x) for x∈[0,π2] is as follows.
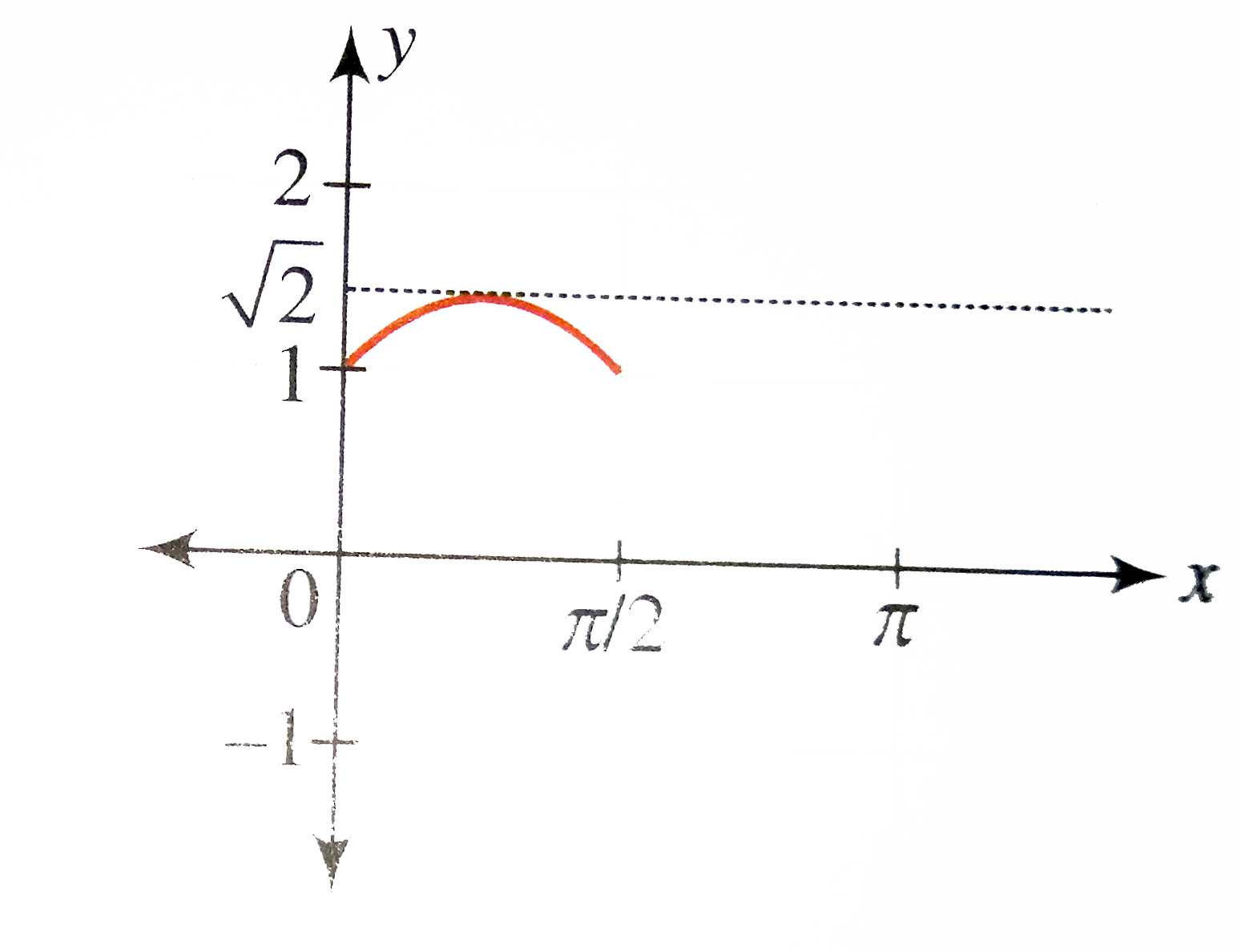
Since the period of y=f(x) is π/2, the graph is repeated as shown in the following figure.
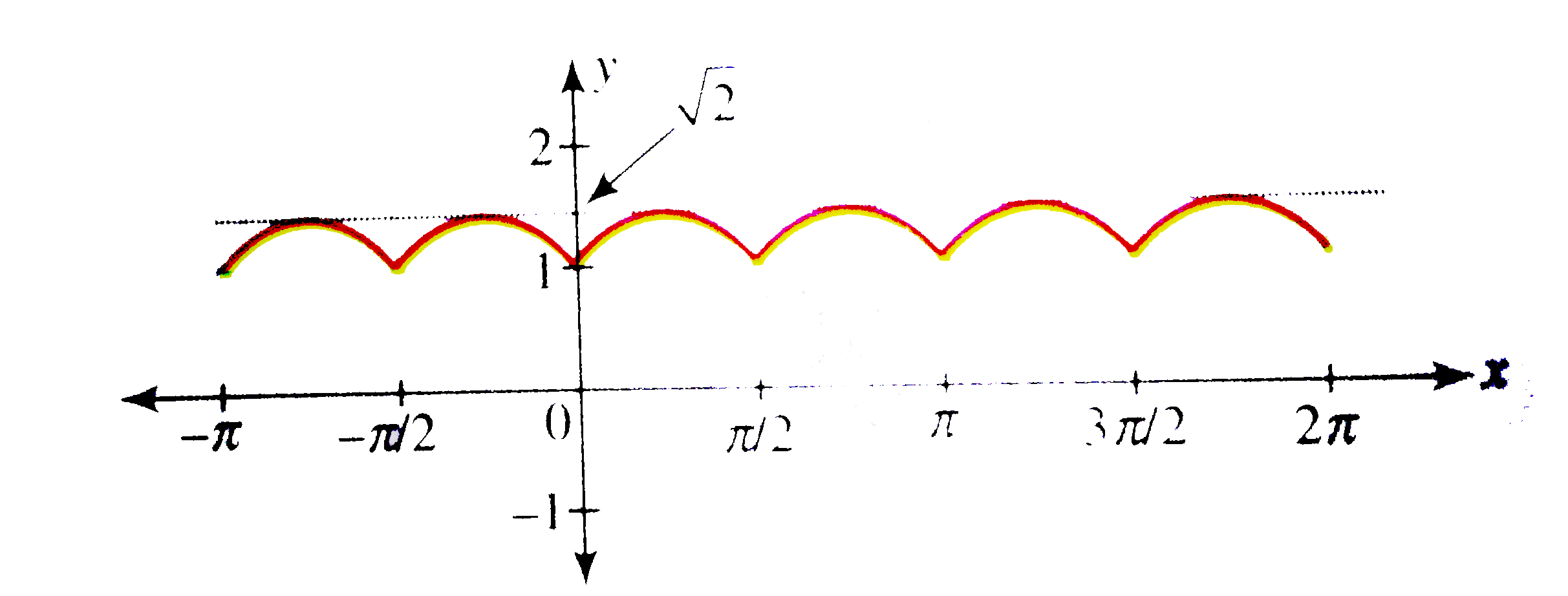
From the graph, the range of f(x) is [1,√2].
|
Topper's Solved these Questions
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBook:CENGAGE ENGLISHChapter:GRAPHS OF TRIGONOMETRIC FUNCTIONSExercise:Exercises
Explore 22 Videos
- GRAPHS OF ELEMENTARY FUNCTIONS Book:CENGAGE ENGLISHChapter:GRAPHS OF ELEMENTARY FUNCTIONS Exercise:EXERCISES
Explore 34 Videos
- HIGHT AND DISTANCE Book:CENGAGE ENGLISHChapter:HIGHT AND DISTANCE Exercise:Archives
Explore 3 Videos
Similar Questions
Draw the graph of f(x)=x|x|.
View SolutionDraw the graph of f(x)=|tanx|+|cotx|.
View SolutionDraw the graph of f(x)=esinx.
View SolutionDraw the graph of f(x)=√sinx.
View SolutionDraw the graph of f(x)=(x+2)|x−1|.
View SolutionDraw the graph of y=|sinx|+sin|x|.
View SolutionDraw the graph of y=cos2x.
View SolutionDraw the graph of y=x−sinx
View SolutionDraw the graph of f(x)=|x−1|x−1.
View SolutionDraw the graph of f(x)=xcosx−sinx,x∈[−3π,3π]
View Solution
