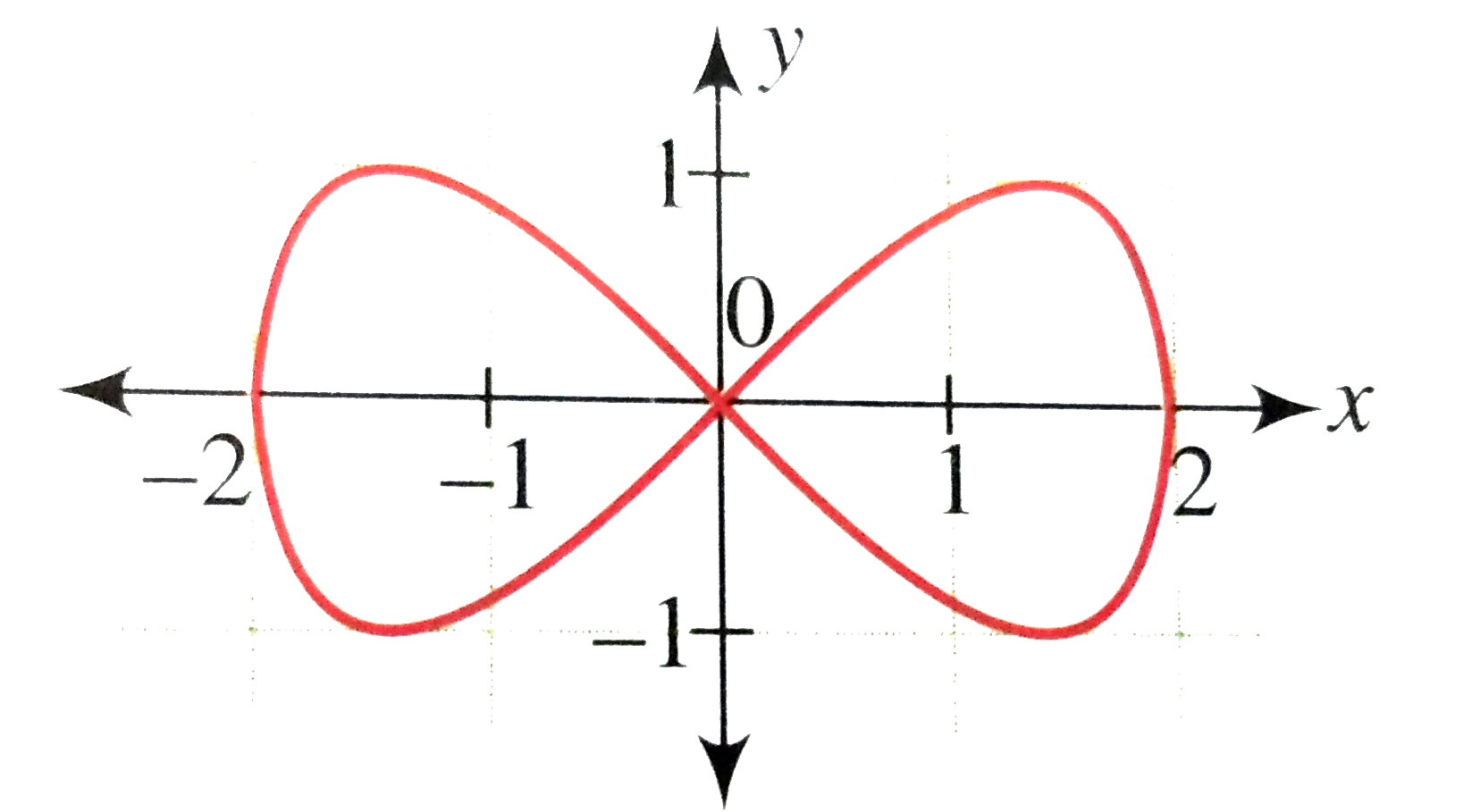
Draw the graph of the relation 4y2=x2(4−x2)Solution in Bengali
We have 4y2=x2(4−x2)
∴y=±12√x2(4−x2)
∴y=±x2√4−x2
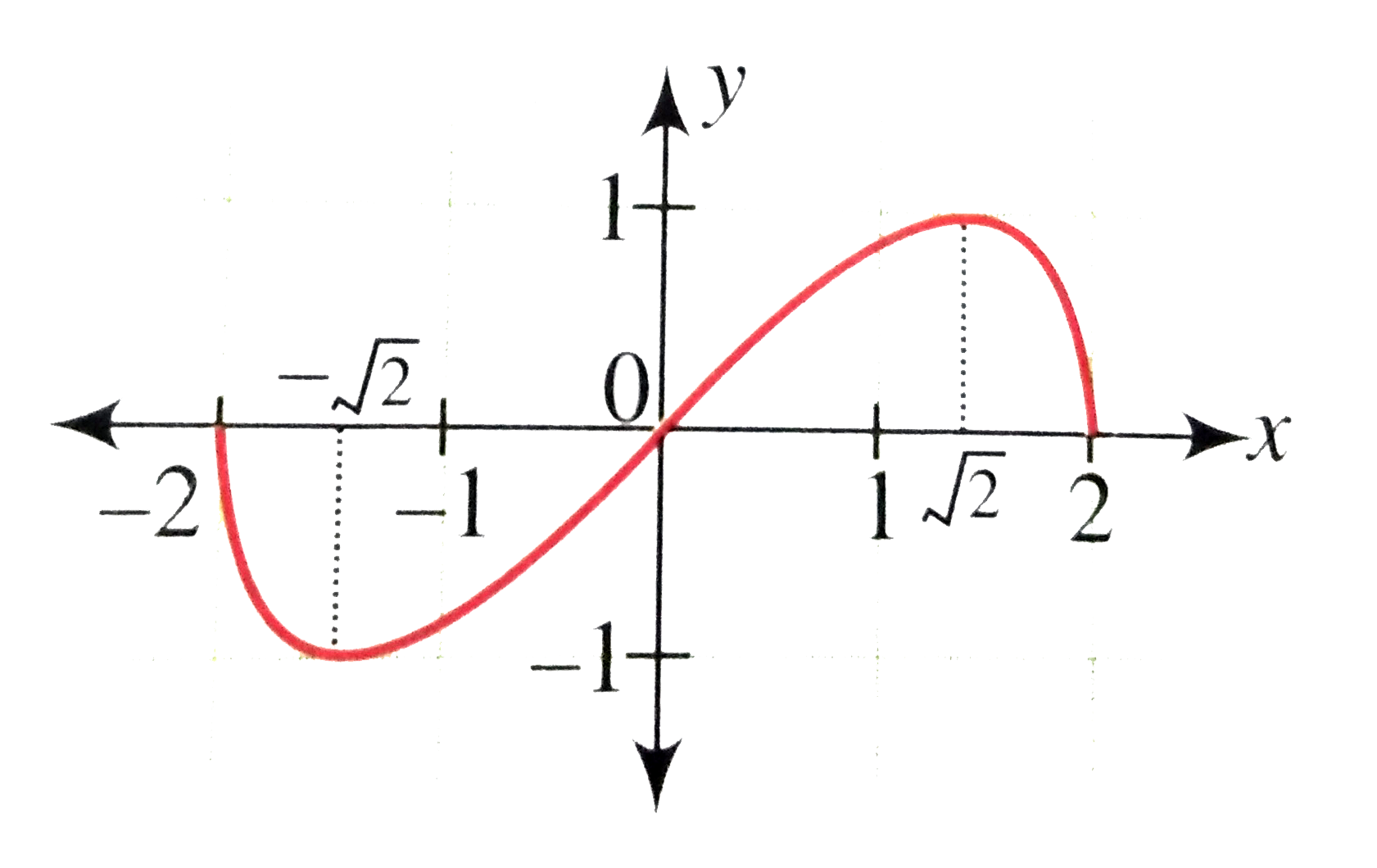
Let us first draw the graph of y=f(x)=x2√4−x2
Clearly, the domain is [−2.2]
Now, f(0)=f(−2)=f(2)=0
Also for x<0,f(x)<0 and for x>0,f(x)>0
Now dydx=12√4−x2−x2x√4−x2
⇒4−x2=x2
⇒x=±√2
Since f(x)>0 for x<0 and f(0)=f(2)=0,x=√2 is the point of maxima and x=−√2 is the point of minima.
f(√2)=1,f(−√2)=−1
Also f(x) is an odd function.
Hence, the graph of the function is as shown in the following figure.
Graph of y=−x1√4−x2 can be obtained by reflecting the above graph in the x-axis.
Hence, the graph of the relation 4y2=x2(4−x2) is a follows.
Topper's Solved these Questions
- CURVE TRACINGBOOK - CENGAGE PUBLICATIONCHAPTER - CURVE TRACINGEXERCISE - EXERCISES
22 Videos
- COORDINATE SYSYEM BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - JEE Main
6 Videos
- DEFINITE INTEGRATION BOOK - CENGAGE PUBLICATIONCHAPTER - DEFINITE INTEGRATION EXERCISE - JEE ADVANCED
37 Videos
Similar Questions
Find the derivative of y=sin2x−cosx
View SolutionThe lines p(p2+1)x−y+q=0 and (p2+1)2x+(p2+1)y+2q=0 are perpendicular to a common line for
View SolutionLet f be a non-negative function defined on the interval [0,1]. If ∫x0√1−(f′(t))2dt=∫x0f(t)dt,0≤x≤1,and f(0)=0, then
View SolutionDraw the graph of the relation y2=x2(1−x)
View SolutionDraw the graph of the relation 4y2=x2(4−x2)
View SolutionDraw the graph of the relation (y−x)2=x3
View SolutionDraw the graph of the relation y=|x|√1−x2
View SolutionDraw the graph of the relation y2=x5(2−x)
View SolutionDraw the graph of the function x2−4x+2 and from the graph examine the continuity of the function at x = - 2.
View SolutionDraw the graph of the relation y2=x2(1−x)
View SolutionDraw the graph of the relation 4y2=x2(4−x2)
View SolutionDraw the graph of the relation (y−x)2=x3
View SolutionDraw the graph of the relation y=|x|√1−x2
View SolutionDraw the graph of the relation y2=x5(2−x)
View SolutionDraw the graph of the function f(x)=x2−4x+2
View SolutionDraw the graph of the relation y2=x2(1−x)
View Solution

