Draw the graph of y=[x]+√x−[x], where[⋅] denotes the greatest ineger function.
y=f(X)=[x]+√x−[x]
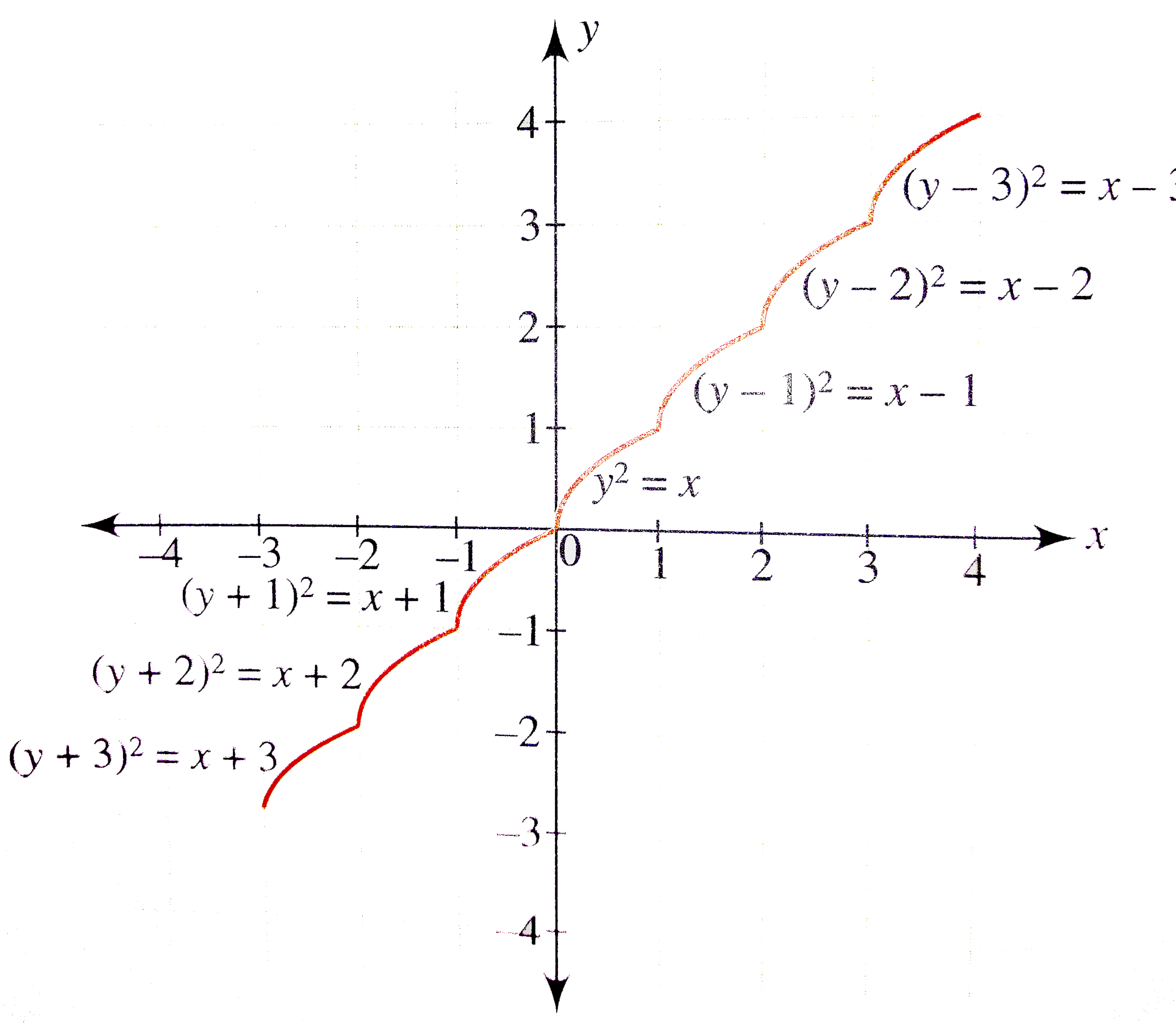
For 0≤x<1,y=√x, the graph of which is part of parabola y2=x lying above the x-axis.
For 1≤x<2,y=1+√x−1, the graph of which is part of the parabola (y−1)2=x−1 lying above the axis of the parabola y=1.
Thus, all the branches of y=f(x) are part of different parabolas.
Also we can see that in each interval y=f(x) is an increasing function.
Hence the graph ofy=f(x) is as shown in the following figure.
Topper's Solved these Questions
- GRAPHS OF ELEMENTARY FUNCTIONS Book:CENGAGEChapter:GRAPHS OF ELEMENTARY FUNCTIONS Exercise:Exercise
Explore 34 Videos
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBook:CENGAGEChapter:GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSExercise:Exercise
Explore 13 Videos
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBook:CENGAGEChapter:GRAPHS OF TRIGONOMETRIC FUNCTIONSExercise:Exercise
Explore 22 Videos
Similar Questions
Let f(x)=[x]+√x−[x], where [.] denotes the greatest integer function. Then
View SolutionDraw the graph of f(x)=[√x],x∈[0,16), where [⋅] denotes the greatest ineger function.
View SolutionDraw the graph of f(x)=[√x],x∈[0,16), where [⋅] denotes the greatest ineger function.
View SolutionDraw the graph of [y]=sinx,x∈[0,2π] where [⋅] denotes the greatest integer function
View SolutionDraw the graph of [y]=sinx,x∈[0,2π] where [⋅] denotes the greatest integer function
View SolutionSketch the curves
(iii) y=∣∣[x]+√x−[x]∣∣
(where [.] denotes the greatest integer function).
(where [.] denotes the greatest integer function).
View SolutionSketch the curves
(iii) y=∣∣[x]+√x−[x]∣∣
(where [.] denotes the greatest integer function).
(where [.] denotes the greatest integer function).
View SolutionSketch the curves
(ii) y=[x]+√x−[x]
(where [.] denotes the greatest integer function).
View SolutionDraw the graph of f(x)=cosπ[x], where [⋅] represents the greatest integer function. Find the period of the function.
View SolutionDraw the graph of f(x)=cosπ[x], where [⋅] represents the greatest integer function. Find the period of the function.
View Solution

