Draw the graph of y=xex. Find the range of the function. Also find the point of inflection.Solution in Bengali
We have y=f(x)=xex
Clearly, the domain of the function is R.
f(0)=−0
and f(x)=0 when x=0
f′(x)=ex+xex=ex(1+x)
f′(x)>0 for x<−1, where f(x) increases
f′(x)<0 for x<−1, where f(x) decreases
f′(x)=0∴x=−1
Also at x=−1,dydx, Changes sign from negative to positive, hence x=−1 is the point of minima,
f(−1)=−e−1=−1/e
When x→∞,f(x)→∞
Also limx→−∞xex=xx→−∞e−x=1x→−∞−e−x=0
So x-axis is an asymptote.
Thus, in (−∞,−1),f(x) decreases from 0+→−1/e
In (1,∞),f(x) increases, intersecting the x-axis at x=0
f''(x)=ex(2+x)
f''(x)=0∴x=−2
So x=−2 is the point of inflection.
From the above discussion, the graph of the function is as follows:
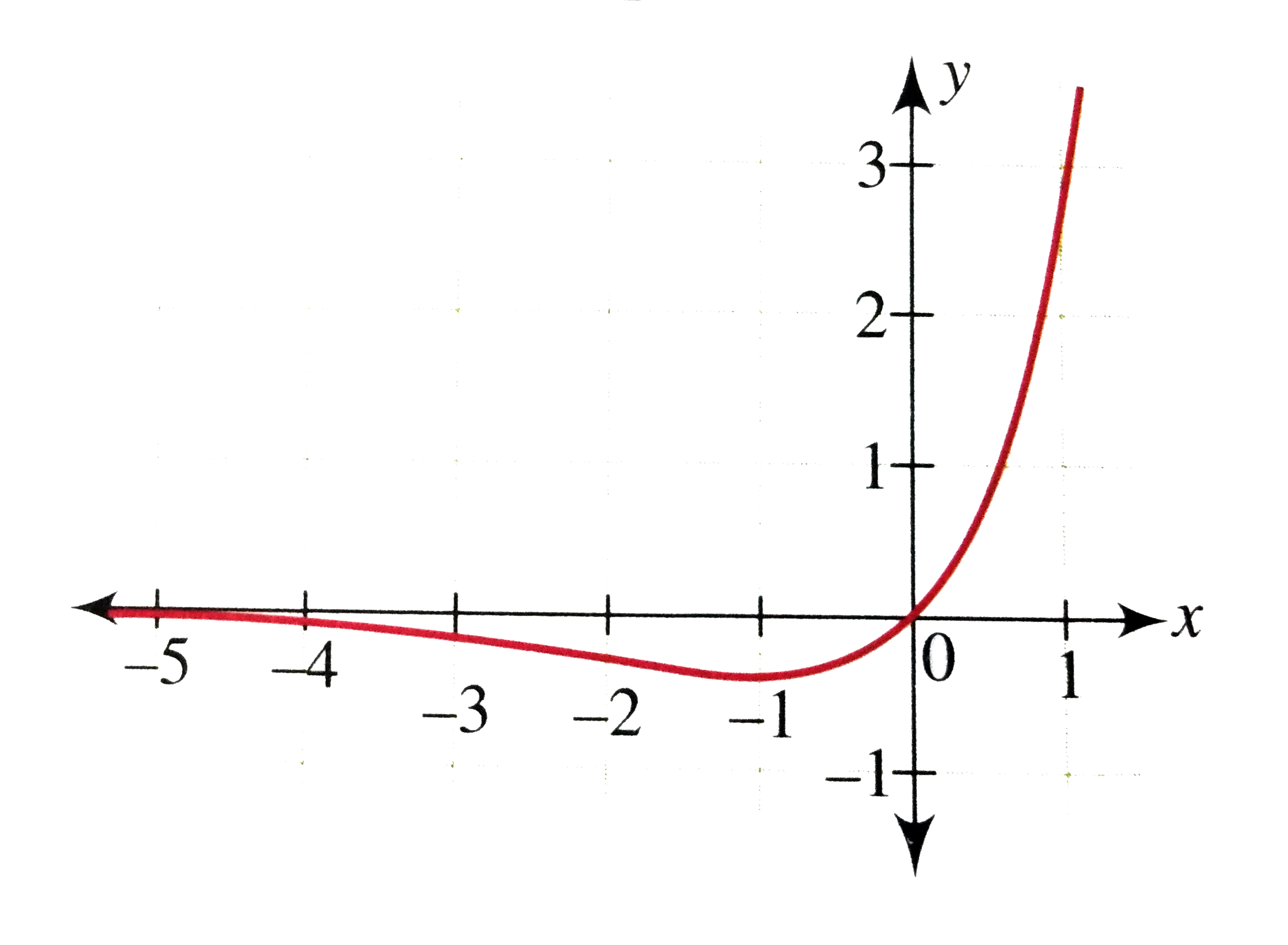
Range of the function is [f(−1),∞) or [−e−1,∞).
Topper's Solved these Questions
- CURVE TRACINGBOOK - CENGAGE PUBLICATIONCHAPTER - CURVE TRACINGEXERCISE - EXERCISES
22 Videos
- COORDINATE SYSYEM BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - JEE Main
6 Videos
- DEFINITE INTEGRATION BOOK - CENGAGE PUBLICATIONCHAPTER - DEFINITE INTEGRATION EXERCISE - JEE ADVANCED
37 Videos
Similar Questions
Find the derivative of y=sin2x−cosx
View SolutionThe lines p(p2+1)x−y+q=0 and (p2+1)2x+(p2+1)y+2q=0 are perpendicular to a common line for
View SolutionLet f be a non-negative function defined on the interval [0,1]. If ∫x0√1−(f′(t))2dt=∫x0f(t)dt,0≤x≤1,and f(0)=0, then
View SolutionFind the points of local maxima or minima and corresponding local maximum and minimum values of f(x)=x ex . Also, find the points of inflection, if any:
View SolutionDraw the graph of y=sin−1(logex). Also find the point of inflection.
View SolutionDraw the graph of y=xex. Find the range of the function. Also find the point of inflection.
View SolutionDraw the graph of f(x)=ex1+ex. Also find the point of inflection.
View SolutionDraw the graph of f(x)=2x+3x2/3 and discuss the type of non-differentiability for the function. Also find the point of inflection.
View SolutionDraw the graph of y=xex.Also
(i) Find the range of the functionf
(ii) Find the point of inflection.
(iii)Find the values of k if 1xex=k has two distinct real roots
View SolutionDraw the graph of y=sin−1(logex). Also find the point of inflection.
View SolutionDraw the graph of y=xex. Find the range of the function. Also find the point of inflection.
View SolutionDraw the graph of f(x)=ex1+ex. Also find the point of inflection.
View SolutionDraw the graph of f(x)=2x+3x2/3 and discuss the type of non-differentiability for the function. Also find the point of inflection.
View SolutionDraw the graphs of y=x and y=−x in the same graph. Also, find the coordinates of the point where the two lines intersect.
View SolutionDraw the graphs of y=x and y=−x in the same graph. Also, find the coordinates of the point where the two lines intersect.
View SolutionFind the intervals in which the graphs of the following functions are concave or convex and locate the points of inflection :
y=x1+x2
View Solution

