Evaluate ∫x1/3(2+x1/2)2dx.
The correct Answer is:3x4/3+37x7/3+2411x11/6+C
To evaluate the integral I=∫x1/3(2+x1/2)2dx, we will follow these steps:
Step 1: Expand the integrand
First, we expand the expression (2+x1/2)2:
(2+x1/2)2=22+2⋅2⋅x1/2+(x1/2)2=4+4x1/2+x
Thus, we can rewrite the integral as:
I=∫x1/3(4+4x1/2+x)dx
Step 2: Distribute x1/3
Now, we distribute x1/3 across the expanded terms:
I=∫(4x1/3+4x1/3⋅x1/2+x1/3⋅x)dx
This simplifies to:
I=∫(4x1/3+4x(1/3+1/2)+x(1/3+1))dx
Calculating the exponents:
1/3+1/2=5/6and1/3+1=4/3
So the integral becomes:
I=∫(4x1/3+4x5/6+x4/3)dx
Step 3: Integrate each term
Now we can integrate each term separately:
1. For 4x1/3:
∫4x1/3dx=4⋅x1/3+11/3+1=4⋅x4/34/3=3x4/3
2. For 4x5/6:
∫4x5/6dx=4⋅x5/6+15/6+1=4⋅x11/611/6=2411x11/6
3. For x4/3:
∫x4/3dx=x4/3+14/3+1=x7/37/3=37x7/3
Step 4: Combine the results
Now we combine all the integrated terms:
I=3x4/3+2411x11/6+37x7/3+C
where C is the constant of integration.
Final Answer
Thus, the final result for the integral is:
I=3x4/3+2411x11/6+37x7/3+C
First, we expand the expression (2+x1/2)2:
(2+x1/2)2=22+2⋅2⋅x1/2+(x1/2)2=4+4x1/2+x
Thus, we can rewrite the integral as:
I=∫x1/3(4+4x1/2+x)dx
Now, we distribute x1/3 across the expanded terms:
I=∫(4x1/3+4x1/3⋅x1/2+x1/3⋅x)dx
This simplifies to:
I=∫(4x1/3+4x(1/3+1/2)+x(1/3+1))dx
Calculating the exponents:
1/3+1/2=5/6and1/3+1=4/3
So the integral becomes:
I=∫(4x1/3+4x5/6+x4/3)dx
Now we can integrate each term separately:
1. For 4x1/3:
∫4x1/3dx=4⋅x1/3+11/3+1=4⋅x4/34/3=3x4/3
∫4x5/6dx=4⋅x5/6+15/6+1=4⋅x11/611/6=2411x11/6
∫x4/3dx=x4/3+14/3+1=x7/37/3=37x7/3
Now we combine all the integrated terms:
I=3x4/3+2411x11/6+37x7/3+C
where C is the constant of integration.
Thus, the final result for the integral is:
I=3x4/3+2411x11/6+37x7/3+C
Topper's Solved these Questions
- INDEFINITE INTEGRAL Book:ARIHANT MATHS ENGLISHChapter:INDEFINITE INTEGRAL Exercise:Exercise For Session 1
Explore 15 Videos
- INDEFINITE INTEGRAL Book:ARIHANT MATHS ENGLISHChapter:INDEFINITE INTEGRAL Exercise:Exercise For Session 2
Explore 15 Videos
- HYPERBOLABook:ARIHANT MATHS ENGLISHChapter:HYPERBOLAExercise:Hyperbola Exercise 11 : Questions Asked in Previous 13 Years Exams
Explore 3 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBook:ARIHANT MATHS ENGLISHChapter:INVERSE TRIGONOMETRIC FUNCTIONSExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 8 Videos
Similar Questions
Evaluate the following integration
∫dx√x+1−√x
View SolutionSolve the following integration
∫dx1+sinx
View SolutionMatching the information given in the three columns of the following table column 1, 2 and 3 contain conics, equations of tangents in the conics and points of contact, respectively.
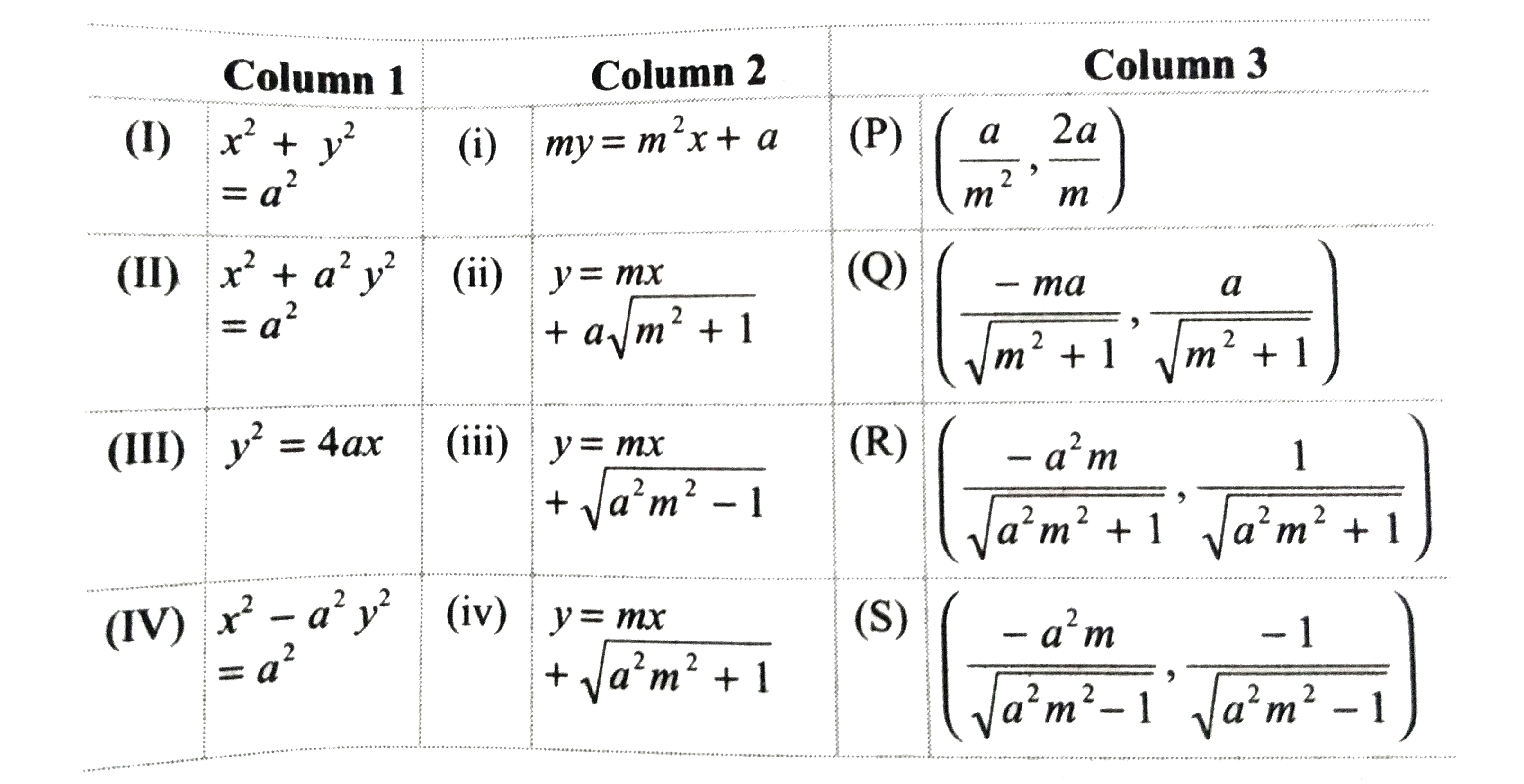
Q. The tangent to a suitable conic (column 1) at (√3,12) is found to be √3x+2y=4, then which of the following options is the correct combination?
View SolutionIf α=3sin−1(611andβ=3cos−1(49), where the inverse trigonometric functions take only the principal values, then the correct options (s) is (are)
View SolutionEvaluate: ∫x2(x−1)3(x+1)dx
View SolutionEvaluate: ∫dxx23(1+x23)
View SolutionEvaluate: ∫x2(x−1)3(x+1) dx
View SolutionEvaluate: ∫ex(1x2−2x3)dx
View Solutionनिमिन्लिखित समाकलनो को ज्ञात कीजिये
(i) ∫x3−1x2dx(int(x^((2)/(3))+1)dx(iii)int(x^((2)/(3))+2e^(x)-(1)/(x))dx
View Solutionनिम्नलिखित समाकलनों को ज्ञात कीजिए:
(i) ∫x3−1x2dx (ii) ∫(x23+1)dx
(iii) ∫(x23+2ex−1x)dx
View SolutionEvaluate the following integrals :
(i)∫x2−4(x2+1)(x2+2)(x2+3)dx (ii)∫1(x+1)(x2+1)2dx
(iii)∫1x3(x2+1)2dx
View SolutionEvaluate :∫dxx2(x3+1)23
View SolutionEvaluate : ∫dxx2(x3+1)23
View SolutionFind the following integrals:
(i) ∫x3−1x2dx (ii) ∫(x23+1)dx (iii) ∫(x32+2ex−1x)dx
View SolutionFind the following integrals:
(i) ∫x3−1x2dx (ii) ∫(x23+1)dx (iii) ∫(x32+2ex−1x)dx
View SolutionFind the following integrals:
(i) ∫x3−1x2dx (ii) ∫(x23+1)dx (iii) ∫(x32+2ex−1x)dx
View Solution
