Evaluate: ∫1sinx+√3cosx dx
The correct Answer is:12log∣∣∣tan(x2+π6)∣∣∣+C
To evaluate the integral ∫1sinx+√3cosxdx, we will follow a systematic approach.
1. Rewrite the Integral:
We start with the integral:
I=∫1sinx+√3cosxdx
2. Multiply and Divide by 2:
To simplify the expression, we multiply and divide by 2:
I=∫22(sinx+√3cosx)dx=∫2sinx+√3cosx⋅12dx
3. Use the Angle Sum Identity:
We recognize that sinx+√3cosx can be expressed in terms of a single sine function using the angle sum identity:
sinx+√3cosx=2(sinxcosπ3+cosxsinπ3)=2sin(x+π3)
Therefore, we can rewrite the integral as:
I=∫12sin(x+π3)dx
4. Integrate:
The integral of 1sinu is ln|tanu2|+C. Thus, we have:
I=12∫1sin(x+π3)dx=12ln∣∣
∣∣tan(x+π32)∣∣
∣∣+C
5. Final Result:
Simplifying gives us:
I=12ln∣∣∣tan(x2+π6)∣∣∣+C
Final Answer:
∫1sinx+√3cosxdx=12ln∣∣∣tan(x2+π6)∣∣∣+C
We start with the integral:
I=∫1sinx+√3cosxdx
To simplify the expression, we multiply and divide by 2:
I=∫22(sinx+√3cosx)dx=∫2sinx+√3cosx⋅12dx
We recognize that sinx+√3cosx can be expressed in terms of a single sine function using the angle sum identity:
sinx+√3cosx=2(sinxcosπ3+cosxsinπ3)=2sin(x+π3)
Therefore, we can rewrite the integral as:
I=∫12sin(x+π3)dx
The integral of 1sinu is ln|tanu2|+C. Thus, we have:
I=12∫1sin(x+π3)dx=12ln∣∣
∣∣tan(x+π32)∣∣
∣∣+C
Simplifying gives us:
I=12ln∣∣∣tan(x2+π6)∣∣∣+C
∫1sinx+√3cosxdx=12ln∣∣∣tan(x2+π6)∣∣∣+C
Topper's Solved these Questions
- INDEFINITE INTEGRAL Book:ARIHANT MATHS ENGLISHChapter:INDEFINITE INTEGRAL Exercise:Exercise For Session 4
Explore 25 Videos
- INDEFINITE INTEGRAL Book:ARIHANT MATHS ENGLISHChapter:INDEFINITE INTEGRAL Exercise:Exercise For Session 5
Explore 10 Videos
- INDEFINITE INTEGRAL Book:ARIHANT MATHS ENGLISHChapter:INDEFINITE INTEGRAL Exercise:Exercise For Session 2
Explore 15 Videos
- HYPERBOLABook:ARIHANT MATHS ENGLISHChapter:HYPERBOLAExercise:Hyperbola Exercise 11 : Questions Asked in Previous 13 Years Exams
Explore 3 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBook:ARIHANT MATHS ENGLISHChapter:INVERSE TRIGONOMETRIC FUNCTIONSExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 8 Videos
Similar Questions
∫x2exdx
View SolutionEvaluate the following Integrals :
∫x2(x−1)(x−2)(x−3)dx
View SolutionSolve the following integration
∫dx1+sinx
View SolutionMatching the information given in the three columns of the following table column 1, 2 and 3 contain conics, equations of tangents in the conics and points of contact, respectively.
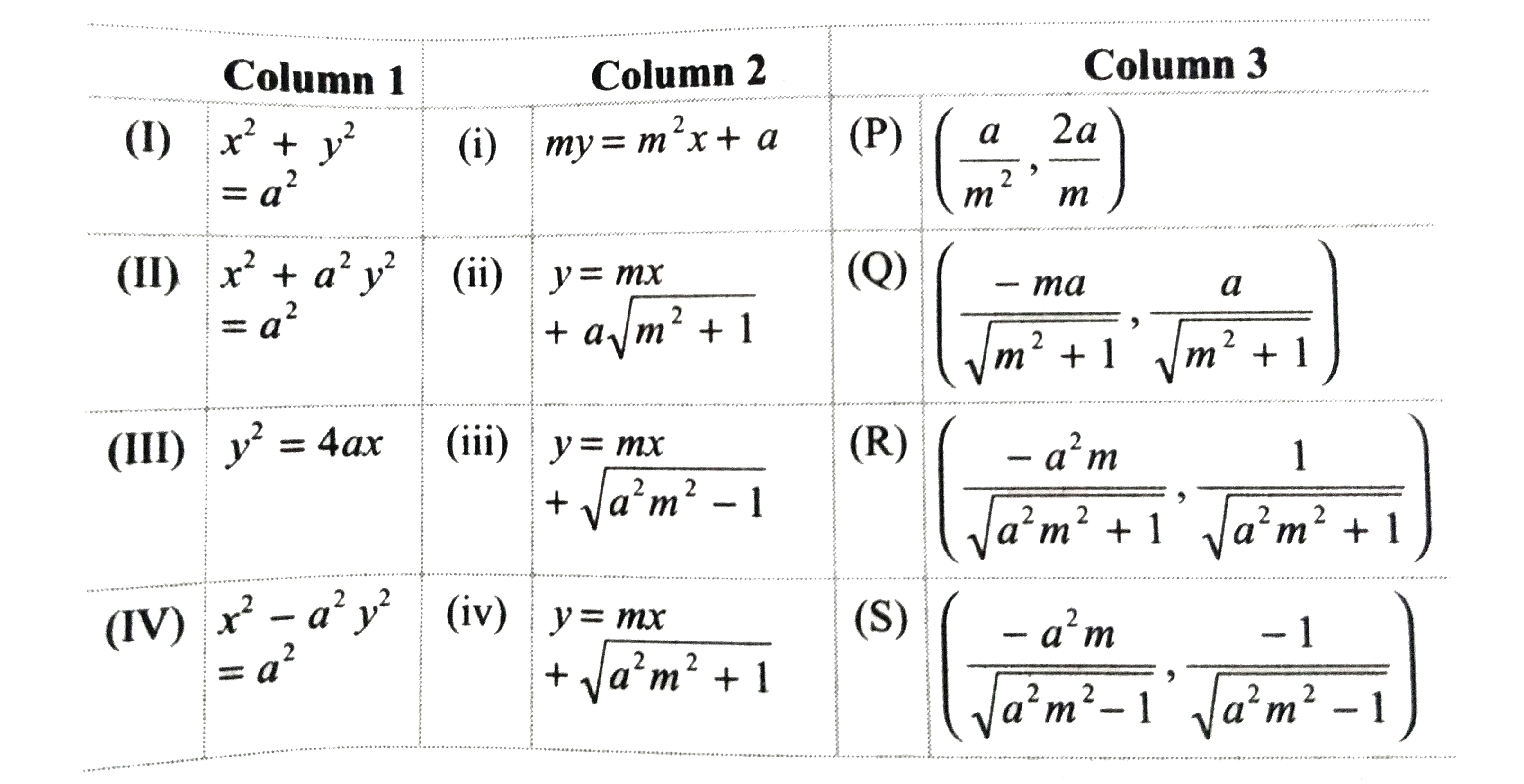
Q. The tangent to a suitable conic (column 1) at (√3,12) is found to be √3x+2y=4, then which of the following options is the correct combination?
View SolutionIf α=3sin−1(611andβ=3cos−1(49), where the inverse trigonometric functions take only the principal values, then the correct options (s) is (are)
View SolutionEvaluate: ∫1cosx−sinx dx
View SolutionEvaluate: ∫1sinx+cosx dx
View SolutionEvaluate: ∫1√3sinx+cosxdx
View SolutionEvaluate: ∫11+sinx+cosxdx
View SolutionEvaluate: ∫1sinx+cosx dx
View SolutionEvaluate: ∫1√3sinx+cosxdx
View SolutionEvaluate: ∫11+sinx+cosx dx
View SolutionEvaluate: ∫11−sinx+cosx dx
View SolutionEvaluate: ∫1cosx−sinx dx
View SolutionEvaluate: ∫1sinx+√3cosx dx
View Solution
