Find the angle between the two tangents from the origin to the circle (x−7)2+(y+1)2=25
The correct Answer is:90∘
Centre of the circle is C(7,-1) and radius , CM=5.
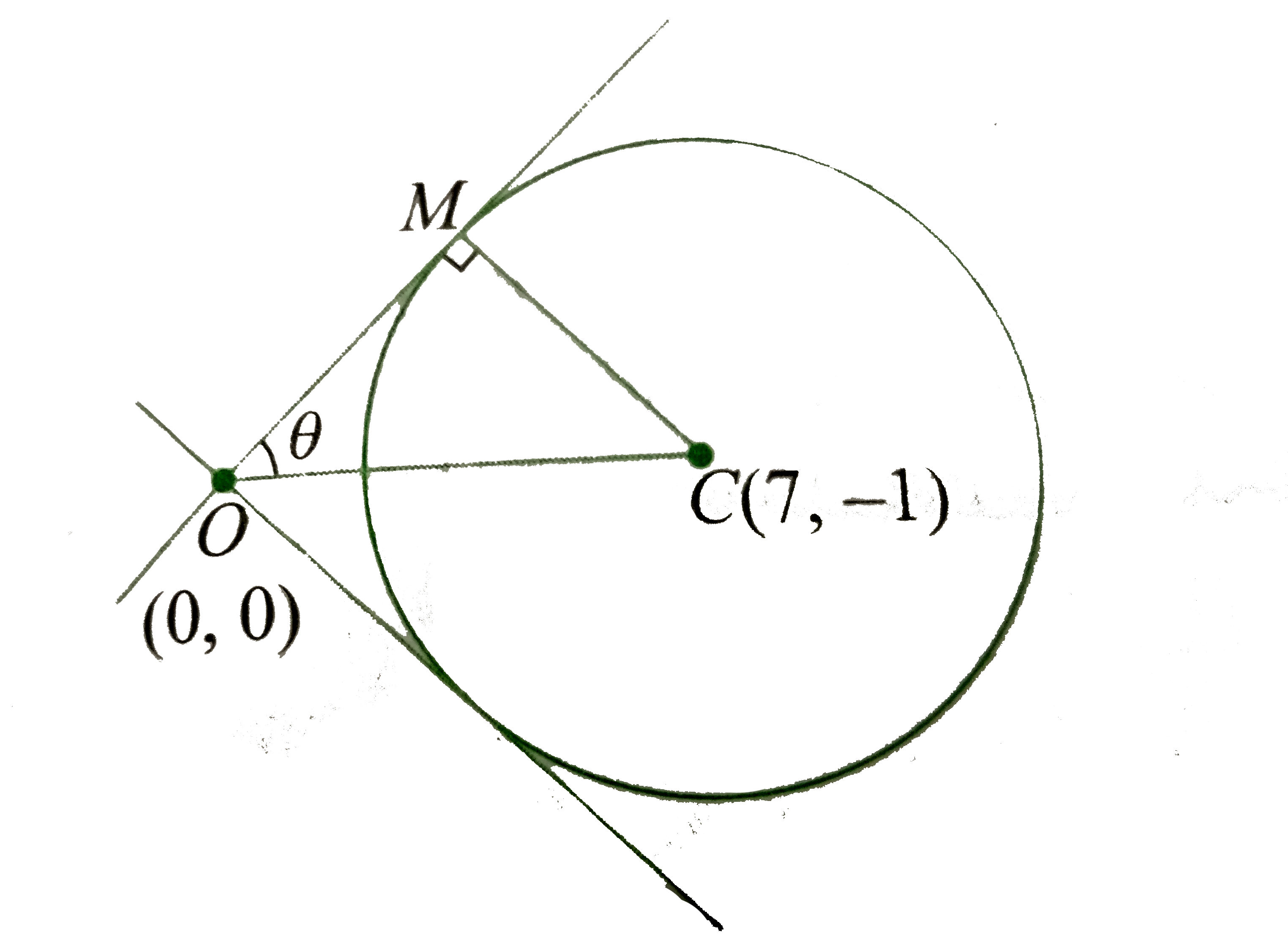
OC=√72+(−1)2=5√2
∴sinθ=CMOC=55√2=1√2
⇒θ=45∘
Hence, angle between tangents is 90∘.
Similar Questions
The angle between the tangents from the origin to the circle (x-7)^2 +(y+1)^2=25 is :
View SolutionFind the angle between the two tangents from the origin to the circle (x−7)2+(y+1)2=25
View SolutionIf two tangents are drawn from a point to the circle x2+y2=32 to the circle x2+y2=16, then the angle between the tangents is :
View SolutionThe angle between the tangents drawn from a point on the director circle x2+y2=50 to the circle x2+y2=25, is
View Solutionमूल बिन्दु से वृत्त (x−7)2+(y+1)2=25 पर खींची गई स्पर्श रेखाओं के मध्य कोण है
View SolutionIf two tangents are drawn from a point to the circle x2+y2=32 to the circle x2+y2=16, then the angle between the tangents is
View SolutionFind the angle between the two tangents from the origin to the circle (x−7)2+(y+1)2=25
View SolutionFind the angle between the two tangents from the origin to the circle (x−7)2+(y+1)2=25
View Solution

