Find the area bounded by the curve x2=4y and the straight line x=4y−2.
The correct Answer is:98 sq. units
Given curves x2=4yandx=4y−2 intersect, when
x2=x+2
or x2−x−2=0
or x=2,−1
⇒ y=1,1/4
Hence, points of intersection area A(−1,1/4),B(2,1)
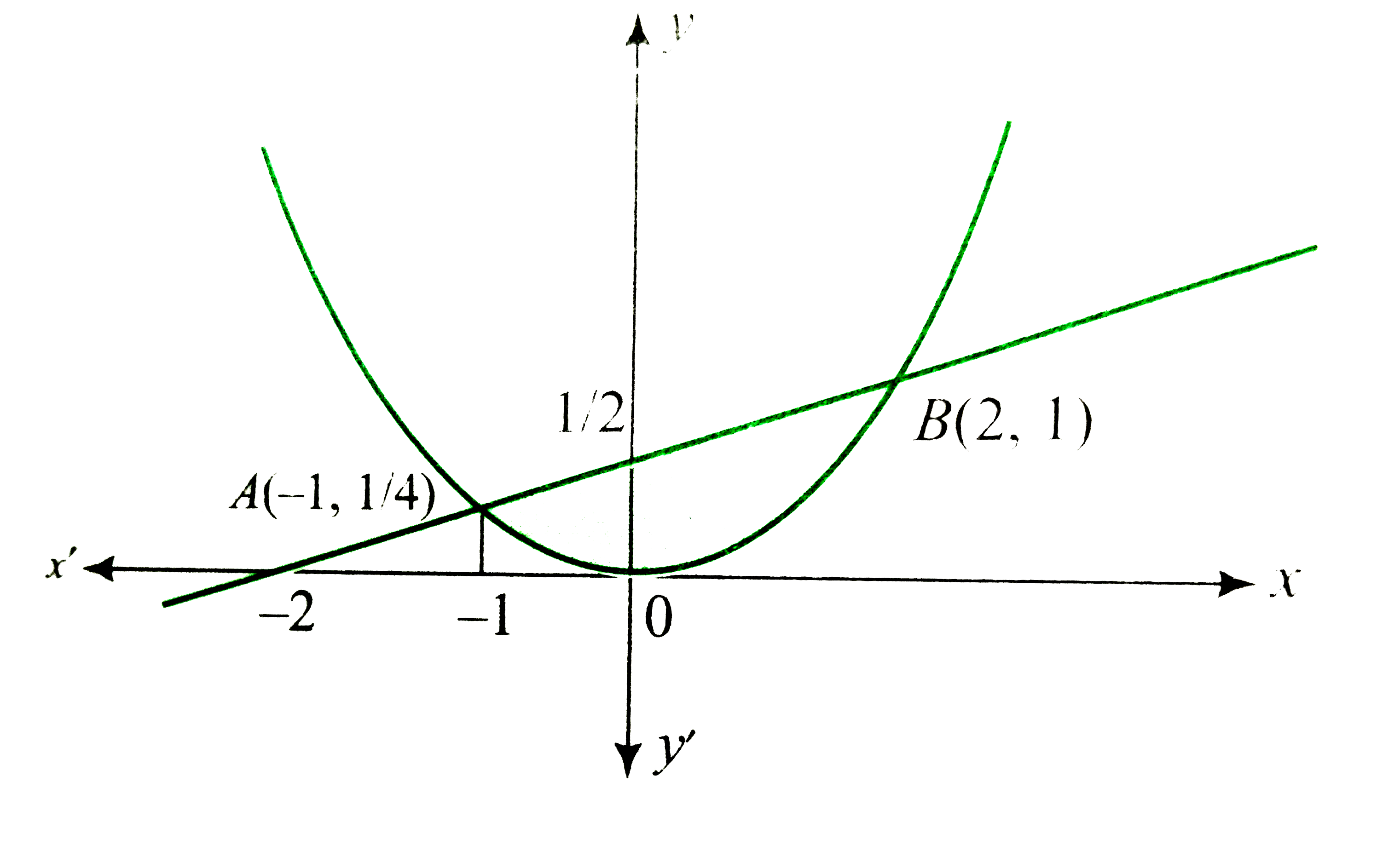
Required area = Shaded region in the figure
=∫2−1(x+24−x24)dx
=14[x22+2x−x33]2−1
=14[(2+4−83)−(12−2+13)]
=14[103−(−76)]=14[276]=9/8 sq. units.
Topper's Solved these Questions
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.3
7 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Single)
40 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.1
9 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Question Bank
29 Videos
- AREA UNDER CURVESBOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank
20 Videos
Similar Questions
Find the continuous function f where (x4−4x2)≤f(x)≤(2x2−x3) such that the area bounded by y=f(x),y=x4−4x2. then y-axis, and the line x=t, where (0≤t≤2) is k times the area bounded by y=f(x),y=2x2−x3,y−aξs, and line x=t(where0≤t≤2).
View SolutionArea enclosed by the curve y=f(x) defined parametrically as x=1−t21+t2,y=2t1+t2 is equal to
View SolutionFind the area of the smaller part of the circle x2+y2=a2cut off by the line x=a√2
View SolutionIf the slope of the tangent to the curve 2(x−y3)4=x2(1+x3)5 at the point (1, -1) is t, then find the value of [|t|].
View SolutionThe area enclosed by g(x),x=−3,x=5 and x -axis where g(x) is the inverse of f(x)=x3+3x+1 is
View SolutionThe area of the region bounded by the curve x2=4y and the straight line x=4y−2 is
View SolutionThe area of the region bounded by the curve x2=4y and the straight line x=4y−2 is
View SolutionFind the area bounded by the curve x2=4y and the line x=4y−2.
View Solutionx2=4y বক্র, x = 2 সরলরেখা এবং x-অক্ষ দ্বারা সীমাবদ্ধ অঞ্চলের ক্ষেত্রফল (বর্গ এককে) হয়—
View SolutionThe area bonuded by the curve x2=4y and the line x=4y−2 is
View SolutionThe area of the region bounded by the curve x2=4y and the straight line x=4y−2 is
View SolutionThe area of the region bounded by the curve x2=4y and the straight line x=4y−2 is
View SolutionFind the area bounded by the curve x2=4y and the straight line x=4y−2.
View SolutionThe area of the region bounded by the curve x2=4y and the straight line x=4y−2 is
View SolutionFind the area bounded by the curve x2=4y and the straight line x=4y−2.
View SolutionThe area of the region bounded by the curve x2=4y and the straight line x=4y−2 is ……
View Solution

