Find the area bounded by the curve y=(x−1)(x−2)(x−3) lying between the ordinates x=0andx=3.Solution in Tamil
y=f(x)=(x−1)(x−2)(x−3)
y=0, then x=1,2,3.
So, graph of the function is as shown in the following figure.
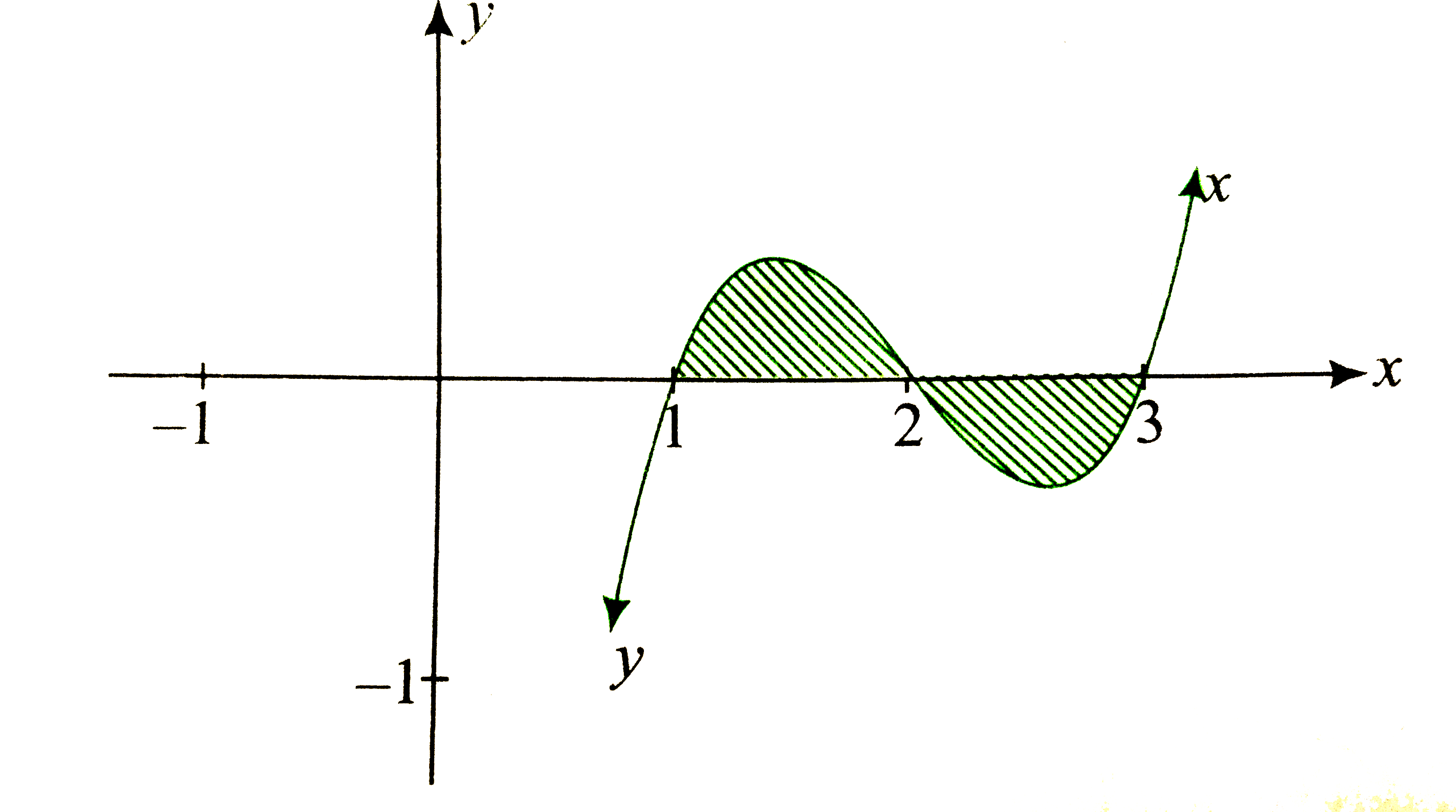
Since f(2−x)=−f(2+x)
2∫1f(x)dx=∣∣
∣∣3∫2f(x)dx∣∣
∣∣
∴ Area of the shaded region,
A=22∫1f(x3−6x2+11x−6)dx
=2[x44−2x3+11x22−6x]21
=2×14=12
Topper's Solved these Questions
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.1
9 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.2
13 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Multiple Correct Answer Type
4 Videos
- AREA UNDER CURVESBOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank
10 Videos
Similar Questions
Find the area of the smaller part of the circle x2+y2=a2 cut off by the line x=a√2.
View SolutionFind the area lying in the first quadrant and bounded by the curve y=x3 and the line y=4x.
View SolutionEquation of a line which is tangent to both the curve y=x2+1 and y=x2 is y=√2x+12 (b) y=√2x−12 y=−√2x+12 (d) y=−√2x−12
View SolutionThe area of the region (s) enclosed by the curves y=x2 and y=√|x| is
View SolutionFind the area bounded by the curve y=(x−1)(x−2)(x−3) lying between the ordinates x=0andx=3.
View SolutionFind the area bounded by the curve y=log x, waxis and the ordinates x=(1)/(2) and x=(3)/(2)
View SolutionThe area bounded by the curve y=(x-1)(x-2)(x-3) and x -axis lying between the ordinates x=0 and x=4 is
View SolutionFind the area bounded by the curve y=4x−x2, the x-axis and the ordinates x=1 and x=3.
View SolutionThe area bounded by the curve y=(x−1)(x−2)(x−3) and X-axis lying between ordinates x=0 and x=3 is
View SolutionThe area in square unit bounded by the curves y=x3,y=x2 and the ordinates x=1, x=2 is
View SolutionFind the area bounded by the curve y=(x−1)(x−2)(x−3) lying between the ordinates x=0andx=3.
View SolutionFind the area of the region bounded by the curves y=x2+2,y=x,x=0,andx=3.
View SolutionFind the area bounded by the curve y=(x−1)(x−2)(x−3) lying between the ordinates x=0andx=3.
View SolutionFind the area bounded by the curve y=(x−1)(x−2)(x−3) lying between the ordinates x=0andx=3.
View SolutionThe area bounded by the curve y=(x−1)(x−2)(x−3) and x-axis lying between the ordinates x=0andx=4 is
View Solution

