Find the area bounded by y=x2andy=x1/3 for x∈[−1,1].
Video Solution
Text Solution
The correct Answer is:32 sq. units
Solving given curves we get x2=x1/3
∴ x=0orx=1
Required area, A=0∫−1[x2−x1/3]dx+1∫0[x1/3−x2]dx
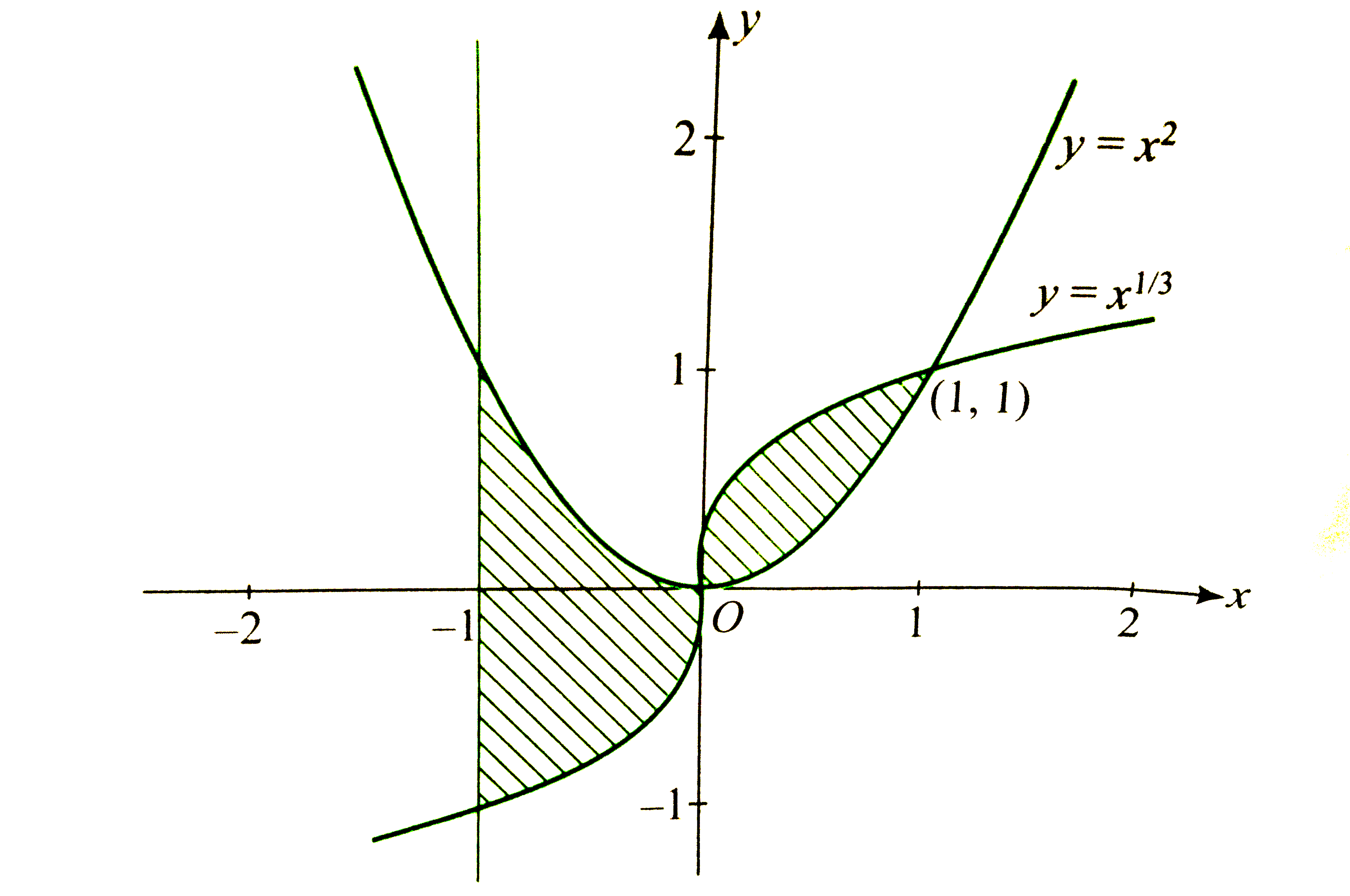
=[x33−3x4/34]0−1+[3x4/34−x33]10
=−[−13−34]+[34−13]=32 sq. units.
|
Topper's Solved these Questions
- AREABook:CENGAGEChapter:AREAExercise:Exercise 9.3
Explore 7 Videos
- AREABook:CENGAGEChapter:AREAExercise:Exercise (Single)
Explore 40 Videos
- AREABook:CENGAGEChapter:AREAExercise:Exercise 9.1
Explore 9 Videos
- APPLICATIONS OF DERIVATIVESBook:CENGAGEChapter:APPLICATIONS OF DERIVATIVESExercise:Question Bank
Explore 29 Videos
- AREA UNDER CURVESBook:CENGAGEChapter:AREA UNDER CURVESExercise:Question Bank
Explore 20 Videos
Similar Questions
Knowledge Check
The area bounded by y=x2 and y=1−x2 is
A√8/3B16/3C32/3D16/3
Find the area bounded by the curves y=√1−x2 and y=x3−x without using integration.
View SolutionFind the area bounded by the curves y=√1−x2andy=x3−x.Also find the ratio in which they-axis divided this area.
View SolutionFind the area bounded by y = x - 1 and (y−1)2=4(x+1)
View SolutionFind the area bounded by the curves y2−x−1=0 and y2+x−1=0.
View SolutionThe area bounded by y=3−|3−x| and y=6|x+1| is
View Solutionfind the area bounded by the curves y=x2+1 and x+y=3
View SolutionFind the area bounded by the curve |x|+y=1 and axis of x.
View Solution
