Find the area of smaller region founded by the ellipse x29+y24=1 and the straight line x3+y2=1Solution in Punjabi
The correct Answer is:45 sq unit
Step by step video solution for Find the area of smaller region founded by the ellipse (x^(2))/9+(y^(2))/4=1 and the straight line x/3+y/2=1 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Find the area of the smaller region bounded by the ellipse x29+y24=1 and the line x3+y2=1
View SolutionFind the area of the smaller region bounded by the ellipse x29+y24=1 and the line x3+y2=1.
View Solutionरेखाओं y=|x| तथा दीर्घवृत x29+y24=1 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
View SolutionFind the area of the smaller region bounded by the ellipse x29+y24=1 and the line x3+y2=1
View SolutionFind the area of the smaller region bounded by the ellipse x29+y24=1 and the line x3+y2=1.
View SolutionFind the area of the smaller region bounded by the ellipse x29+y24=1 and the line x3+y2=1.
View SolutionFind the area of the smaller region bounded by the ellipse x29+y24=1 and the line x3+y2=1.
View SolutionUsing the method of integration, find the area of the smaller region bounded by the ellipse x29+y24=1 and the line x3+y2=1.
View SolutionFind the area of the smaller region bounded by the ellipse x29+y24=1 and the line x3+y2=1.
View SolutionFind the area of smaller region bounded by the ellipse x29+y24=1 and straight line x3+y2=1.
View SolutionFind the area of the smaller region bounded by the ellipse x29+y24=1 and the line x3+y2=1
View SolutionFind the area of the smaller region bounded by the ellipse x29+y24=1 and the line x3+y2=1
View SolutionFind the area of the smaller region bounded by the ellipse x29+y24=1and the line x3+y2=1.
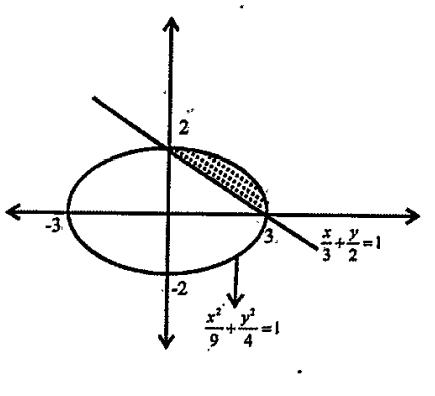
View SolutionFind the area of the smaller region bounded by the ellipse x29+y24=1 and the line x3+y2=1.
View SolutionFind the area of smaller region founded by the ellipse x29+y24=1 and the straight line x3+y2=1
View SolutionFind the area of smaller region founded by the ellipse x29+y24=1 and the straight line x3+y2=1
View Solution
