Find the area of the region bounded by the limits x=0,x=π2,andf(x)=sinx,g(x)=cosx.
Video Solution
Text Solution
The correct Answer is:2(√2−1) sq. units
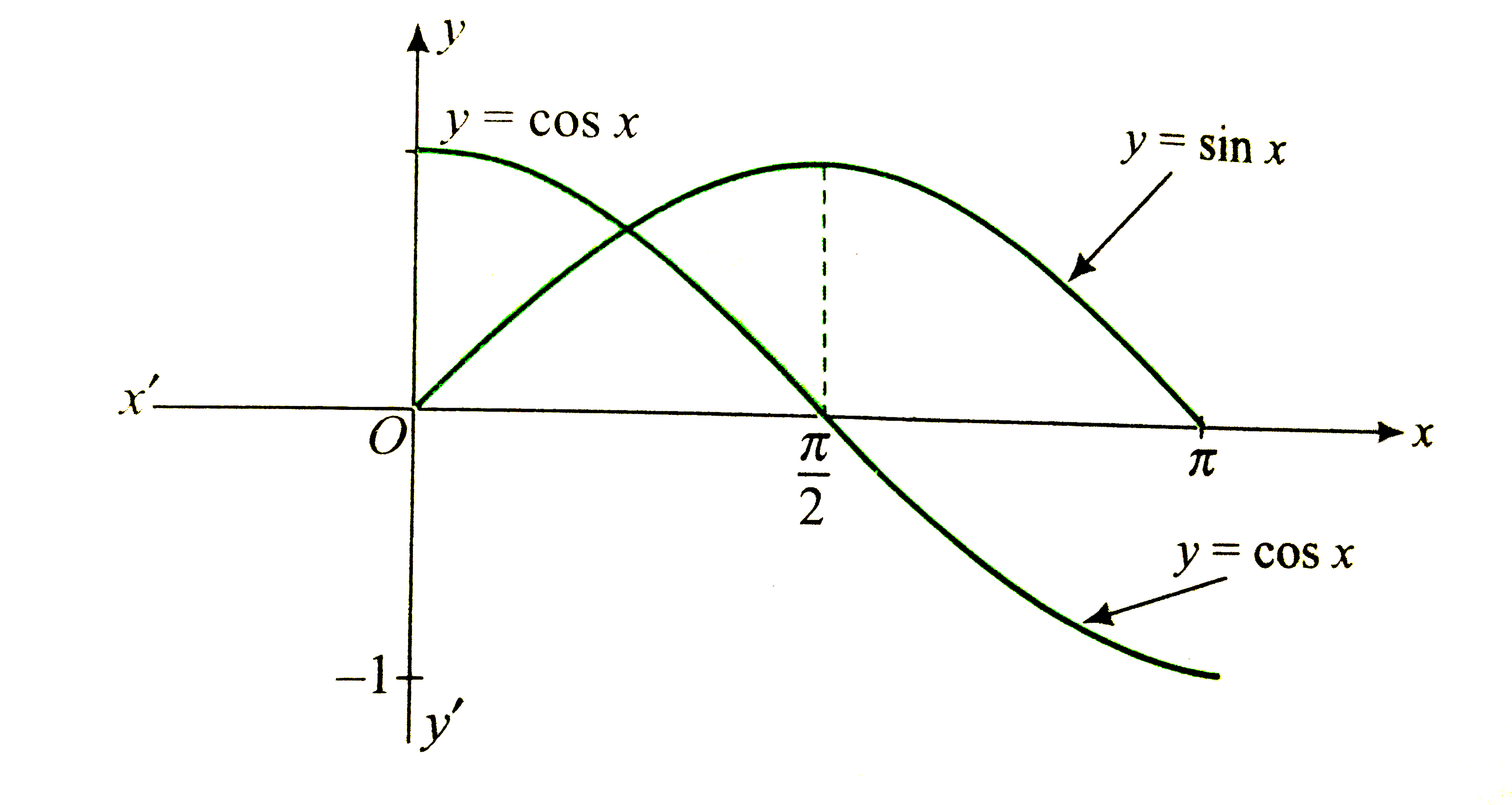
Required area =∫π/20|sinx−cosx|dx
=2∫π/40(cosx−sinx)dx
=2|sinx+cosx|π/40
=2(1√2+1√2−1)=2(√2−1) sq. units.
|
Similar Questions
Find the area of the region bounded by the curves y=x2+2,y=x,x=0,andx=3.
View SolutionFind the area of the region bounded by the limits x=0,x=π2,andf(x)=sinx,g(x)=cosx.
View SolutionFind the area of the region bounded by
y=|cosx|,y=0,x=−πandx=π
View SolutionFind the area of the region bounded by
y=ex,y=0,x=0andx=ln2
View SolutionFind the area of the region bounded by
y= sin x and y= cos x between x=0 and x=π2
View SolutionFind the area of the region bounded by
y=cosxandy=sin2x between x=0andx=π2
View SolutionFind the area bounded by
y=sinx,y=0,x=π2
View SolutionFind the area of the region bounded by y=sinx,y=cosx and ordinates x=0,x=π/2.
View Solution
