Find the area of the triangle, whose vertices are (2,1), (4,5) and (6,3).
3
6
9
12
The correct Answer is:B
Area of triangle =12[xx(y2−y3)+x2(y3−y1)+x3(y1−y2)]
=12[2(5−3)+4(3−1)+6(1−5)]=12(4+8−24)=−6
But the area of triangle connot be negative
∴ Area of triangle = 6 square units
Similar Questions
Using the method of integration find the area of the triangle ABC, coordinates of whose vertices are A(2,0),B(4,5) and C(6,3).
View SolutionThe vertices of a triangle are the points (2,1) , (−2,3) and (4,5). Find the equation of its sides.
View Solutionउस त्रिभुज का क्षेत्रफल ज्ञात कीजिये जिसके शीर्ष क्रमश: (2,3),(4,5) और (6,2) है।
View SolutionFind the area of triangle whose vertices are (1,2), (3,4),(1/2,1/4).
View SolutionUsing the method of integration , find the area of the ΔABC,co-ordinates of whose vertices are A(2,0),B(4,5) and C(6,3).
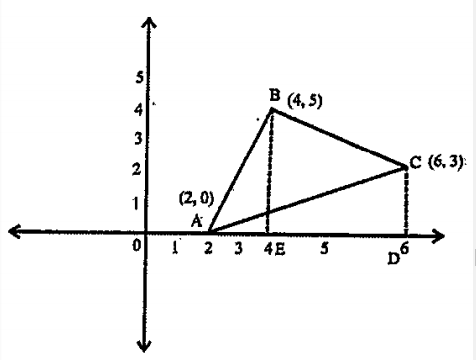
View Solutionਇਨਟਿਗਰੇਸ਼ਨ ਵਿਧੀ ਦਾ ਉਪਯੋਗ ਕਰਦੇ ਹੋਏ ਇੱਕ ਇਸ ਤਰ੍ਹਾਂ ਦੇ ਤ੍ਰਿਭੁਜ ABC, ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ਜਿਸਦੇ ਸਿਖਰਾਂ ਦੇ ਨਿਰਦੇਸ਼ਕ A(2,0),B(4,5),C(6,3) ਹੈ।
View SolutionFind the area of the triangle, whose vertices are (2,1), (4,5) and (6,3).
View SolutionFind the area of that triangle whose vertices are (−4,3),(−2,1)and(5,2).
View Solution