Find the capacity of a glass which is in the shape of frustum of height 14 cm and diameters of both circular ends are 4 cm and 2 cm.
308/3 cm3
298/21 cm3
112 cm3
398/21 cm3
The correct Answer is:A
To find the capacity of the glass in the shape of a frustum, we will calculate the volume using the formula for the volume of a frustum of a cone.
1. Identify the given dimensions:
- Height (h) of the frustum = 14 cm
- Diameter of the top circular end (D1) = 4 cm, so the radius (R1) = D1/2 = 4/2 = 2 cm
- Diameter of the bottom circular end (D2) = 2 cm, so the radius (R2) = D2/2 = 2/2 = 1 cm
2. Use the volume formula for a frustum:
The volume V of a frustum of a cone is given by the formula:
V=13πh(R21+R1R2+R22)
3. Substitute the values into the formula:
- R1=2 cm
- R2=1 cm
- h=14 cm
- Using π≈227
Now substituting the values:
V=13×227×14×(22+2×1+12)
4. Calculate R21+R1R2+R22:
- R21=22=4
- R1R2=2×1=2
- R22=12=1
- Therefore, R21+R1R2+R22=4+2+1=7
5. Substitute back into the volume formula:
V=13×227×14×7
6. Simplify the expression:
- The 7 in the numerator and denominator cancels out:
V=13×22×14
7. Calculate the final volume:
- First calculate 22×14=308
- Then divide by 3:
V=3083 cm3
Final Answer:
The capacity of the glass is 3083 cm³ or approximately 102.67 cm³.
- Height (h) of the frustum = 14 cm
- Diameter of the top circular end (D1) = 4 cm, so the radius (R1) = D1/2 = 4/2 = 2 cm
- Diameter of the bottom circular end (D2) = 2 cm, so the radius (R2) = D2/2 = 2/2 = 1 cm
The volume V of a frustum of a cone is given by the formula:
V=13πh(R21+R1R2+R22)
- R1=2 cm
- R2=1 cm
- h=14 cm
- Using π≈227
V=13×227×14×(22+2×1+12)
- R21=22=4
- R1R2=2×1=2
- R22=12=1
- Therefore, R21+R1R2+R22=4+2+1=7
V=13×227×14×7
- The 7 in the numerator and denominator cancels out:
V=13×22×14
- First calculate 22×14=308
- Then divide by 3:
V=3083 cm3
The capacity of the glass is 3083 cm³ or approximately 102.67 cm³.
Topper's Solved these Questions
- SURFACE AREAS AND VOLUMESBook:MTG IIT JEE FOUNDATIONChapter:SURFACE AREAS AND VOLUMESExercise:EXERCISE (INTEGER/NUMERICAL VALUE TYPE)
Explore 10 Videos
- STATISTICSBook:MTG IIT JEE FOUNDATIONChapter:STATISTICSExercise:Olympiad/HOTS Corner
Explore 12 Videos
- TRIANGLES Book:MTG IIT JEE FOUNDATIONChapter:TRIANGLES Exercise:Olympiad /HOTS Corner
Explore 15 Videos
Similar Questions
247 Three cubes of side 4 cm each are joined end to end to form a cuboid. The surface area of theresulting cuboid and total surface area of the three cubes are in the ratio:(B) 7:3(C) 7:9(D) 9:7
View SolutionThe average score of Sehwag in 10 innings was 77 runs. In the 11th inning he had scored zero runs. The overall average score of Sehwag in all the 11 innings was
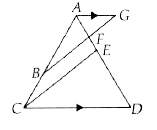
View SolutionIn the given figure (not drawn to scalse ) , AG is parallel to CD and AG=27CD . The point B on AC is such that BC=27AC . If the line BG meets AD at F and the line through C is parallel to BG which meets AD at E , then find the value of FGEC .
View Solutionपानी पीने वाला एक गिलास 14 सेमी ऊँचाई वाले एक शंकु के छिन्नक के आकार का है | दोनों वृत्ताकार सिरों के व्यास 4 सेमी और 2 सेमी है | इस गिलास की धारिता ज्ञात कीजिए |
View SolutionA drinking glass is in the shape of a frustum of a cone of height 14 cm, The diameters of its two circular ends are 16 cm and 12 cm. Find the capacity of the glass.
View SolutionThe radii of the circulr ends of a frustum of height 6 cm are 14 cm and 6 cm respetively. Find the slant height of the frustum.
View SolutionIf the radii of the circular ends of a frustum shaped object which is 30 cm high are 14 cm and 7 cm. Find the total surface area and capacity of the object.
View Solutionपानी पीने वाला एक गिलास 14 सेमी ऊंचाई वाले एक शंकु के छिन्नक के आकार का है। दोनों वृत्ताकार सिरों के व्यास 4 सेमी और 2 सेमी हैं। इस गिलास की धारिता ज्ञात कीजिए।
View Solutionपानी पीने वाला एक गिलास 14 सेमी ऊंचाई वाले एक शंकु के छिन्नक के आकार का है । दोनों वृत्ताकार सिरों के व्यास 4 सेमी और 2 सेमी है । इस गिलास की धारिता ज्ञात कीजिए ।
View SolutionA drinking glass is in the shape of a first term of a cone of height 14 cm. The diameter of its two circular ends 4 cm and 2 cm. Find the capacity of the glass.
View SolutionA drinking glass is in the shape of a frustum of a cone of height 14 cm. The diameters of its two circular ends are 4 cm and 2 cm. Find the capacity of the glass.
View SolutionA drinking glass is in the shape of a frustum of a cone of height 14cm . The diameters of its two circular ends. are 4cm and 2cm . Find the capacity of the glass.
View SolutionA drinking glass is in the shape of a frustum of a cone of height 14 cm. The diameters of its two circular ends are 4 cm and 2 cm. Find the capacity of the glass.
View SolutionA drinking glass is in the shape of a frustum of a cone of height 14 cm. the diameters of its two circular ends are 4 cm and 2 cm. find the capacity of the glass.
View SolutionA drinking glass is in the shape of a frustum of a cone of height 21 cm. The diameters of its two circular ends are 6 cm and 4 cm. Find the capacity of the glass.
View SolutionThe radii of the circular ends of a frustum of a cone are 14 cm and 8 cm. If the height of the frustum is 8 cm. Find (i) Curved surface area of the frustum
View Solution