Find the coordinates of a point A, where AB is diameter of the circle with centre C (2,-3) and B is the point (3,4).
The correct Answer is:-10
To find the coordinates of point A, where AB is the diameter of the circle with center C (2, -3) and point B is (3, 4), we can follow these steps:
1. Understanding the Relationship:
The center of the circle (C) is the midpoint of the diameter AB. Therefore, we can use the midpoint formula to find the coordinates of point A.
2. Midpoint Formula:
The midpoint M of a line segment with endpoints (x1, y1) and (x2, y2) is given by:
M=(x1+x22,y1+y22)
Here, C (the center) is the midpoint, so we can set:
C(2,−3)=(xA+xB2,yA+yB2)
3. Substituting Known Values:
We know B is (3, 4). Let A be (x_A, y_A). Therefore:
2=xA+32and−3=yA+42
4. Solving for x_A:
From the first equation:
2=xA+32
Multiply both sides by 2:
4=xA+3
Subtract 3 from both sides:
xA=1
5. Solving for y_A:
From the second equation:
−3=yA+42
Multiply both sides by 2:
−6=yA+4
Subtract 4 from both sides:
yA=−10
6. Final Coordinates of Point A:
Thus, the coordinates of point A are:
A(1,−10)
Conclusion:
The coordinates of point A are (1, -10).
The center of the circle (C) is the midpoint of the diameter AB. Therefore, we can use the midpoint formula to find the coordinates of point A.
The midpoint M of a line segment with endpoints (x1, y1) and (x2, y2) is given by:
M=(x1+x22,y1+y22)
Here, C (the center) is the midpoint, so we can set:
C(2,−3)=(xA+xB2,yA+yB2)
We know B is (3, 4). Let A be (x_A, y_A). Therefore:
2=xA+32and−3=yA+42
From the first equation:
2=xA+32
Multiply both sides by 2:
4=xA+3
Subtract 3 from both sides:
xA=1
From the second equation:
−3=yA+42
Multiply both sides by 2:
−6=yA+4
Subtract 4 from both sides:
yA=−10
Thus, the coordinates of point A are:
A(1,−10)
The coordinates of point A are (1, -10).
Topper's Solved these Questions
- LINES (IN TWO - DIMENSIONS)BOOK - OSWAL PUBLICATIONCHAPTER - LINES (IN TWO - DIMENSIONS)EXERCISE - BOARD CORNER (SHORT ANSWER TYPE QUESTION)
14 Videos
- LINES (IN TWO - DIMENSIONS)BOOK - OSWAL PUBLICATIONCHAPTER - LINES (IN TWO - DIMENSIONS)EXERCISE - BOARD CORNER (LONG ANSWER TYPE QUESTION)
2 Videos
- LINES (IN TWO - DIMENSIONS)BOOK - OSWAL PUBLICATIONCHAPTER - LINES (IN TWO - DIMENSIONS)EXERCISE - NCERT EXEMPLAR (EXERCISE - 7.4)
9 Videos
- INTRODUCTION TO TRIGONOMETRY AND TRIGONOMETRIC IDENTITIES BOOK - OSWAL PUBLICATIONCHAPTER - INTRODUCTION TO TRIGONOMETRY AND TRIGONOMETRIC IDENTITIES EXERCISE - BOARD CORNER (Long Solution Type Questions)
6 Videos
- LINES (IN TWO DIMENSIONS) BOOK - OSWAL PUBLICATIONCHAPTER - LINES (IN TWO DIMENSIONS) EXERCISE - CASE - BASED MCQs
15 Videos
Similar Questions
Find the ratio in which the line segment joining the points (1, -3) and (4 , 5) is divided by x- axis . Also find the co-ordinates of this point on x-axiws.
View SolutionIf a≠b≠c,prove that(a,a2),(b,b2),(0,0) will not be collinear.
View SolutionIf (-4,3) and (4,3) are two vertices of an equilateral triangle , then find the coordinates of the third vertex , given that the origin lies in the interior of the triangle.
View SolutionProve that sinA−cosA+1sinA+cosA−1=1secA−tanA
View SolutionRead the following text and answer the following questions on the basis of the same :
Class X students of a secondary school in Krishnagar have been allotted a rectangular plot of a land for gardening activity. Saplings of Gulmohar are planted on the boundary at distance of 1 m from each other in the fig. The students are to sow seeds of flowering plants on the remaining area of the plot.
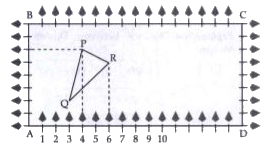
What are the coordinates of A ?
View SolutionFind the coordinates of a point A, where AB is the diameter of a circle whose centre is (2, 3) and B is (1, 4).
View SolutionFind the coordinates of a point A, where AB is a diameter of a circle with centre C(2, -3) and the other end of the diameter is B(1, 4).
View Solutionबिन्दु A के निर्देशांक ज्ञात कीजिए, जहाँ AB एक वृत्त का व्यास है जिसका केन्द्र (2,−3) है तथा B के निर्देशांक (1,4) है ।
View SolutionPoint P is the centre of the circle and AB is a diameter . Find the
coordinates of point B. If coordinates of point A and Pare (2,-3)
and (-2,0) respectively .
View SolutionFind the coordinates of a point A , where AB is the diameter of a circle whose centre is ( 2 , - 3) and B is ( 1 , 4) . (AS4)
View SolutionFind the coordinates of a point A, where AB is the diameter of a circle whose centre is (2, -3) and B is (1, 4).
View SolutionFind the coordinates of a point A, where AB is the diameter of a circle whose centre is (2, -3) and B is (1, 4).
View SolutionFind the coordinates of a point A, where AB is the diameter of a circle whose centre is (2,−3) and B is (1,4).
View SolutionFind the coordinates of a point A, where AB is the diameter of a circle whose centre is (2, -3) and B is (1, 4).
View SolutionFind the coordinates of a point A, where AB is the diameter of a circle whose centre is (2, -3) and B is (1, 4).
View SolutionFind the coordinates of a point A, where AB is the diameter of a circle whose centre is (2, -3) and B is (1, 4).
View Solution
