Find the mean number of heads in three tosses of a fair coin.
The correct Answer is:N/a
Probability of getting head or tail in a toss of one coin is
P(H)=P(T)=12
Sample space in three throw of an unbiased coin is
S={HH,HHT,HTH,THH,THT,TTH,HTT,TTT}
The possible values of random variable X are 0,1,2 or 3.
∴P(X=0)=P (getting all tails)
=P{TTT}=12×12×12=18
P(X=1)=P (getting one head and two tails)
=P(TTH)+P(THT)+P(HTT)
=12×12×12+12×12×12+12×12×12
=18+18+18=38
P(X=2)=P (getting two heads and one tail)
P(HHT)+P(HTH)+P(THH)
=12×12×12+12×12×12+12×12×12
=18+18+18=38
P(X=3)=P (gettting three heads)
=P(HHH)=12×12×12=18
Therefore the required probability distribution is:
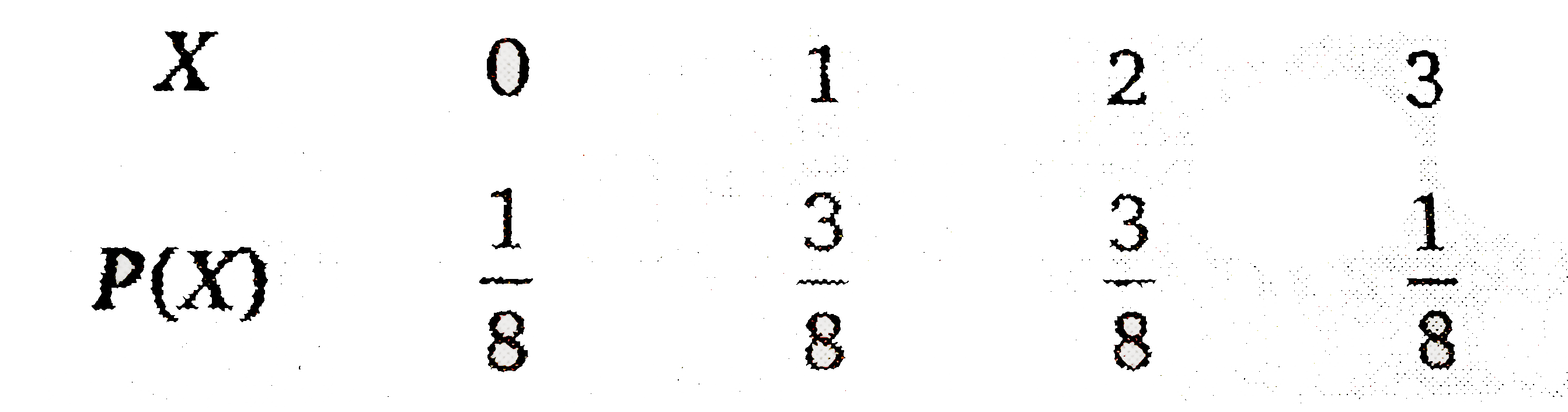
Therefore mean
=∑XP(X)=0×18+1×38+2×38+3×18
=38+68+38=128=32=1.5
Topper's Solved these Questions
- PROBABIILITYBook:NAGEEN PRAKASHAN ENGLISHChapter:PROBABIILITYExercise:Exercise 13.5
Explore 15 Videos
- PROBABIILITYBook:NAGEEN PRAKASHAN ENGLISHChapter:PROBABIILITYExercise:Miscellaneous Exercise
Explore 19 Videos
- PROBABIILITYBook:NAGEEN PRAKASHAN ENGLISHChapter:PROBABIILITYExercise:Exercise 13.3
Explore 14 Videos
- MATRICESBook:NAGEEN PRAKASHAN ENGLISHChapter:MATRICESExercise:Miscellaneous Exerice
Explore 15 Videos
- RELATIONS AND FUNCTIONS Book:NAGEEN PRAKASHAN ENGLISHChapter:RELATIONS AND FUNCTIONS Exercise:Miscellaneous Exercise
Explore 19 Videos
Similar Questions
A die is thrown 6 times. If "getting an even number" is a success, what is the probability of (i) 5 successes? (ii) at least 5 successes? (iii) at most 5 successes?
View SolutionA and B are two events such that P(A)≠0. Find P(B∣A) , if (i) A is a subset of B (ii) A∩B=φ
View SolutionAn urn contains 5 red and 5 black balls. A ball is drawn at random, its colour is noted and is returned to the urn. Moreover, 2 additional balls of the colour drawn are put in the um and then a ball is drawn at random. What is the probability that the second ball is red?
View SolutionLet A=[0100]show that (aI+bA)n=anI+nan−1bA, where I is the identitymatrix of order 2 and n∈N.
View SolutionLet f:R→Rbe defined as f(x)=10x+7. Find the function g:R→Rsuch thatgof=fog=1R
View SolutionFind the mean number of heads in three tosses of a fair coin.
View SolutionFind the mean number of heads in three tosses of a fair coin.
View SolutionFind the mean number of heads in three tosses of a fair coin.
View SolutionFind the mean number of heads in three tosses of a fair coin.
View SolutionFind the mean number of heads in three tosses of a fair coin.
View SolutionFind the mean number of heads in three tosses of a fair coin.
View SolutionFind the mean number of heads in three tosses of a fair coin.
View SolutionFind the mean number of heads in three tosses of a fair coin.
View SolutionFind the mean number of heads in three tosses of a fair coin.
View SolutionFind the mean number of heads in three tosses of a fair coin.
View SolutionFind the mean number of heads in three tosses of a fair coin.
View Solution
