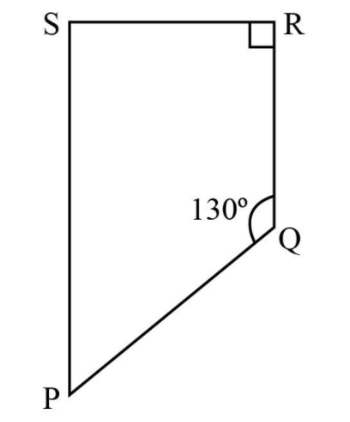
Find the measure of c<Pand<S if −→SP∣∣−−→RQ∈ Fing 3.34. (If you find m<R, is there m or ethano ≠ method of find m<p
To solve the problem of finding the measures of angles P and S given that line segment SP is parallel to line segment RQ, we can follow these steps:
1. Identify the Given Angles:
- We are given that angle Q = 130° and angle R = 90°.
2. Use the Property of Interior Angles:
- Since SP is parallel to RQ, angle P and angle Q are interior angles on the same side of the transversal (line SR). According to the property of parallel lines, the sum of these interior angles is 180°.
- Therefore, we can write the equation:
m∠P+m∠Q=180°
- Substituting the value of angle Q:
m∠P+130°=180°
3. Solve for Angle P:
- Rearranging the equation gives:
m∠P=180°−130°=50°
4. Calculate the Sum of Angles in Quadrilateral:
- In any quadrilateral, the sum of the interior angles is 360°. Therefore, we can write:
m∠P+m∠Q+m∠R+m∠S=360°
- Substituting the known values:
50°+130°+90°+m∠S=360°
5. Solve for Angle S:
- Adding the known angles gives:
50°+130°+90°=270°
- Now substituting back into the equation:
270°+m∠S=360°
- Rearranging gives:
m∠S=360°−270°=90°
Final Answers:
- m∠P=50°
- m∠S=90°
- We are given that angle Q = 130° and angle R = 90°.
- Since SP is parallel to RQ, angle P and angle Q are interior angles on the same side of the transversal (line SR). According to the property of parallel lines, the sum of these interior angles is 180°.
- Therefore, we can write the equation:
m∠P+m∠Q=180°
- Substituting the value of angle Q:
m∠P+130°=180°
- Rearranging the equation gives:
m∠P=180°−130°=50°
- In any quadrilateral, the sum of the interior angles is 360°. Therefore, we can write:
m∠P+m∠Q+m∠R+m∠S=360°
- Substituting the known values:
50°+130°+90°+m∠S=360°
- Adding the known angles gives:
50°+130°+90°=270°
- Now substituting back into the equation:
270°+m∠S=360°
- Rearranging gives:
m∠S=360°−270°=90°
- m∠P=50°
- m∠S=90°
Topper's Solved these Questions
- UNDERSTANDING QUADRILATERALSBook:NCERT ENGLISHChapter:UNDERSTANDING QUADRILATERALSExercise:EXERCISE 3.2
Explore 6 Videos
- SQUARES AND SQUARE ROOTSBook:NCERT ENGLISHChapter:SQUARES AND SQUARE ROOTSExercise:EXERCISE 6.4
Explore 9 Videos
- VISUALISING SOLID SHAPESBook:NCERT ENGLISHChapter:VISUALISING SOLID SHAPESExercise:EXERCISE 10.3
Explore 8 Videos
Similar Questions
Find the measure of each exterior angle of a regular polygon of(i) 9 sides (ii) 15 sides
View SolutionThere are 500 children in a school. For a P.T. drill they have to stand in such a manner that the number of rows is equal to number of columns. How many children would be left out in this arrangement.
View SolutionCan a polyhedron have for its faces(i) 3 triangles?(ii) 4 triangles?(iii) a square and four triangles?
View Solution. Find the measure of ∠P and ∠S if SP || RQ in Fig 3.34. (If you find m∠R, is there more than one method to find m∠P?)
View SolutionIf →p is a unit vector and (→x− →p).(→x+ →p)=80, then find |→x|
View SolutionIf vec p xxvec q = vec m xxvec n and vec p xxvec m = vec q xxvec n show that vec p-vec n is parallel to vec q-vec m where vec p! = Vec n and vec q! = Vec m
View SolutionFind the condition that the lines →r=→a+t(→b×→c),→r=→b+p(→c×→a) may intersect. Accepting that condition , find the point of intersection .
View SolutionShow that the four points P, Q, R, S with position vectors →p, →q, →r, →s respectively such that 5→p−2→q+6→r−9→s=→0, are coplanar. Also find the position vector of the point of intersection of the line segments PR and QS.
View SolutionIf |vec(P) + vec(Q)| = |vec(P) - vec(Q)| , find the angle between vec(P) and vec(Q) .
View SolutionIf veca=m vecb+vec c , find the scalar m.
View SolutionIf vector P,QandR have magnitude 5,12,and 13 units and →P+→Q=→R, the angle between Q and R is
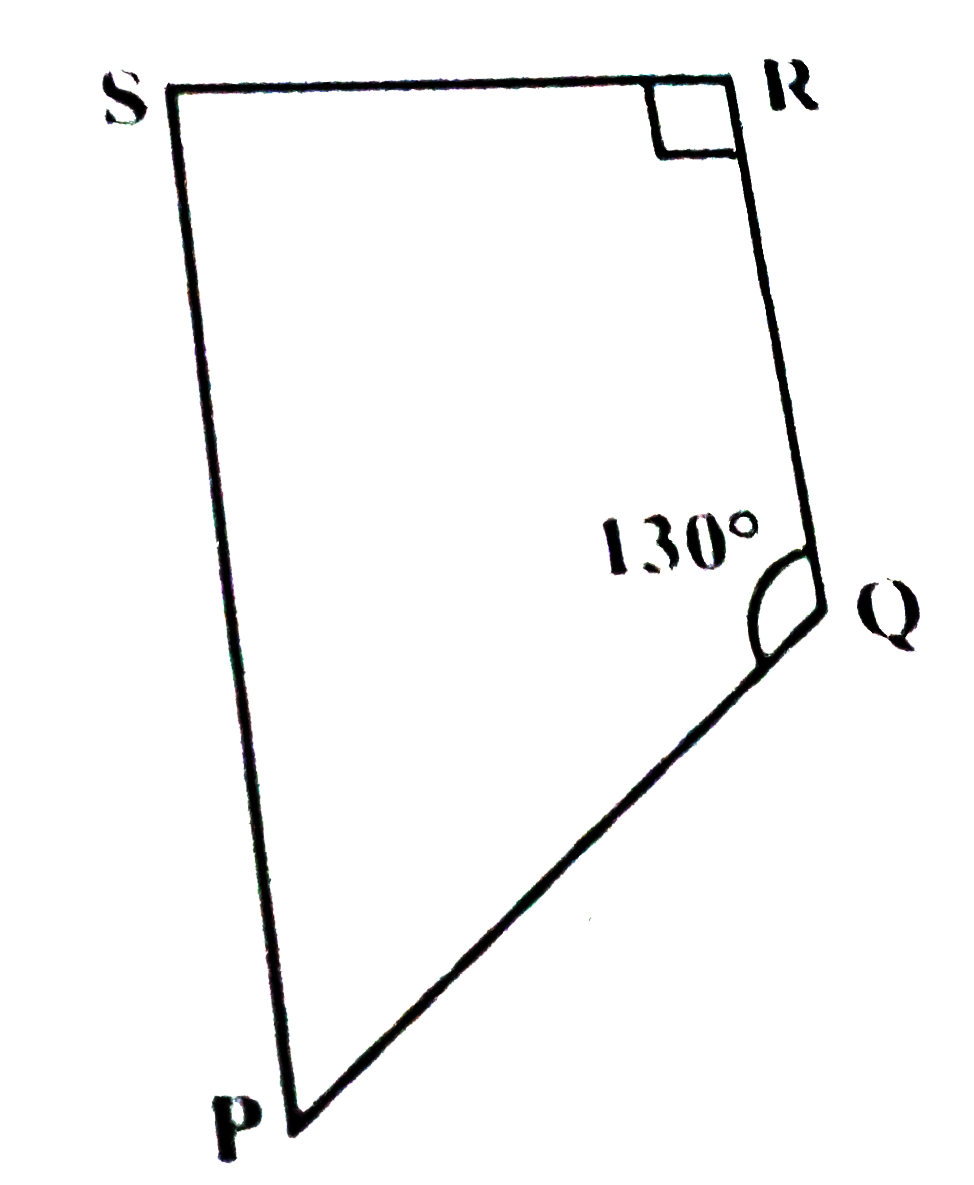
View Solutionआकृति 3.34 में ∠P तथा ∠S की माप ज्ञात कीजिए यदि ¯¯¯¯¯SP□¯¯¯¯¯¯RQ है | (यदि आप m∠R, ज्ञात करते है, तो क्या m∠P को ज्ञात करने की एक से अधिक विधि है ?)
View SolutionFind the area of the given trapezium PQRS in which RQ || SP and PQ ⊥ SP such that RQ = 7m, RS = 13 m and SP = 12 m.
View SolutionIf →p is a unit vector and (→x−→p).(→x+→p)=8 , then find |→x|
View SolutionIf →p is a unit and (→x−→p).(→x+→p)=80 then find |→x|
View Solution