For the polynomial p(x)=12x2−3x+2, find the difference of zeroes.
±2√3
±2√5
±2√2
±3√5
To find the difference of the zeroes of the polynomial p(x)=12x2−3x+2, we can follow these steps:
Step 1: Identify the coefficients
The polynomial is in the standard form ax2+bx+c, where:
- a=12
- b=−3
- c=2
Step 2: Calculate the sum of the zeroes
The sum of the zeroes α+β can be calculated using the formula:
α+β=−ba
Substituting the values of b and a:
α+β=−−312=312=3×2=6
Step 3: Calculate the product of the zeroes
The product of the zeroes αβ can be calculated using the formula:
αβ=ca
Substituting the values of c and a:
αβ=212=2×2=4
Step 4: Calculate the difference of the zeroes
To find the difference of the zeroes α−β, we can use the relationship:
α−β=√(α+β)2−4αβ
Substituting the values we found:
α−β=√(6)2−4×4
Calculating this:
α−β=√36−16=√20
Step 5: Simplify the result
The square root of 20 can be simplified:
√20=√4×5=2√5
Final Answer
Thus, the difference of the zeroes of the polynomial p(x)=12x2−3x+2 is:
α−β=2√5
---
The polynomial is in the standard form ax2+bx+c, where:
- a=12
- b=−3
- c=2
The sum of the zeroes α+β can be calculated using the formula:
α+β=−ba
Substituting the values of b and a:
α+β=−−312=312=3×2=6
The product of the zeroes αβ can be calculated using the formula:
αβ=ca
Substituting the values of c and a:
αβ=212=2×2=4
To find the difference of the zeroes α−β, we can use the relationship:
α−β=√(α+β)2−4αβ
Substituting the values we found:
α−β=√(6)2−4×4
Calculating this:
α−β=√36−16=√20
The square root of 20 can be simplified:
√20=√4×5=2√5
Thus, the difference of the zeroes of the polynomial p(x)=12x2−3x+2 is:
α−β=2√5
Topper's Solved these Questions
- POLYNOMIALSBook:MTG IIT JEE FOUNDATIONChapter:POLYNOMIALSExercise:EXERCISE (Multiple Choice Questions) LEVEL-2
Explore 15 Videos
- POLYNOMIALSBook:MTG IIT JEE FOUNDATIONChapter:POLYNOMIALSExercise:EXERCISE (Match the Following )
Explore 2 Videos
- POLYNOMIALSBook:MTG IIT JEE FOUNDATIONChapter:POLYNOMIALSExercise:NCERT SECTION (EXERCISE 2.4)
Explore 6 Videos
- PAIR OF LINEAR EQUATIONS IN TWO VARIABLESBook:MTG IIT JEE FOUNDATIONChapter:PAIR OF LINEAR EQUATIONS IN TWO VARIABLESExercise:NCERT SECTION (EXERCISE 3.7)
Explore 18 Videos
- PROBABILITYBook:MTG IIT JEE FOUNDATIONChapter:PROBABILITYExercise:Olympiad/HOTS Corner
Explore 26 Videos
Similar Questions
The expression that should be subtracted from 4x4−2x3−6x2+x−5 so that it may be exactly divisible by 2x2+x−2 is
View SolutionList-II gives zeroes (not necessary all) of the polynomials given in List-I, match them correctly.
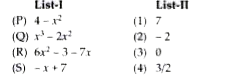
View SolutionVerify that the numbers given alongside of the cubic polynomials below are their zeroes. Also verify the relationship between the zeroes and the coefficients in each case :
2x3+x2−5x+2,1/2,1,−2
View SolutionThe ages of two friends Ani and Biju differ by 3 years. Ani's father Dharam is twice as old as Ani and Biju is twice as old as his sister Cathy. The ages of Cathy and Dharam differ by 30 years. Find the ages of Ani and Biju.
View SolutionA number is chosen at random from 1 to 120, The probability of the number chosen being a multiple of 3 and 15 both is
View SolutionFind the zeros of the polynomial x^(2)+x-p(p+1)
View Solution.The zeroes of the polynomial P(x)=x^2-3x is
View SolutionThe zeroes of the polynomial p(x)=x^2-3x are
View SolutionThe zeros of the polynomial p(x)=x2−3x are
View SolutionThe zeros of the polynomial p(x)=3x2−1 are
View Solutionस्थति में से बहुपद का शून्यक ज्ञात कीजिए:
p(x)=3x−2
View Solutionfind the value of p from the polynomial x2+3x+p if one of the zeroes of the polynomial is 2
View SolutionFind the zero of the polynomial in each of the following cases.
P(x)=3x−2
View SolutionFind the zeroes of the polynomial p(x)=x2−(a+1a)x+1.
View SolutionFind the zeros of the polynomial x2+x−p(p+1)
View SolutionFind zero of the polynomialp(x)=3x+1
View Solution