From a point Q, 13 cm away from the centre of a circle, the length of tangent PQ to the circle is 12 cm. What will be it the radius of the circle (in cm)?
The correct Answer is:5cm
To find the radius of the circle given the distance from point Q to the center O of the circle and the length of the tangent PQ, we can use the Pythagorean theorem. Here’s the step-by-step solution:
Step 1: Identify the Given Information
- Distance from point Q to the center O of the circle (QO) = 13 cm
- Length of the tangent PQ = 12 cm
Step 2: Understand the Geometry
In the right triangle formed by points P, Q, and O:
- OQ is the hypotenuse.
- PQ is one leg (the tangent).
- PO is the other leg (the radius of the circle).
Step 3: Apply the Pythagorean Theorem
According to the Pythagorean theorem:
QO2=PQ2+PO2
Substituting the known values:
132=122+PO2
Step 4: Calculate the Squares
Calculate 132 and 122:
169=144+PO2
Step 5: Solve for PO^2
Rearranging the equation to find PO2:
PO2=169−144
PO2=25
Step 6: Find PO (the Radius)
Taking the square root of both sides to find PO:
PO=√25=5 cm
Conclusion
The radius of the circle is 5 cm.
---
- Distance from point Q to the center O of the circle (QO) = 13 cm
- Length of the tangent PQ = 12 cm
In the right triangle formed by points P, Q, and O:
- OQ is the hypotenuse.
- PQ is one leg (the tangent).
- PO is the other leg (the radius of the circle).
According to the Pythagorean theorem:
QO2=PQ2+PO2
Substituting the known values:
132=122+PO2
Calculate 132 and 122:
169=144+PO2
Rearranging the equation to find PO2:
PO2=169−144
PO2=25
Taking the square root of both sides to find PO:
PO=√25=5 cm
The radius of the circle is 5 cm.
Topper's Solved these Questions
- SAMPLE PAPER 5Book:OSWAL PUBLICATIONChapter:SAMPLE PAPER 5Exercise:Section- B
Explore 3 Videos
- SAMPLE PAPER 5Book:OSWAL PUBLICATIONChapter:SAMPLE PAPER 5Exercise:Section -C
Explore 2 Videos
- SAMPLE PAPER 5Book:OSWAL PUBLICATIONChapter:SAMPLE PAPER 5Exercise:Section -C
Explore 2 Videos
- SAMPLE PAPER 4Book:OSWAL PUBLICATIONChapter:SAMPLE PAPER 4Exercise:Section -C
Explore 8 Videos
- SAMPLE PAPER 6Book:OSWAL PUBLICATIONChapter:SAMPLE PAPER 6Exercise:Section -C
Explore 7 Videos
Similar Questions
Consider the frequency distribution of the heights of 60 students of a class :
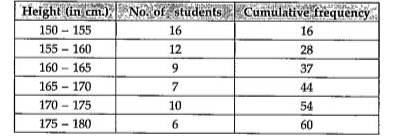
Find the sum of the lower limit of the modal class and the upper limit of the median class.
View SolutionIf Sn denotes the sum of the first n terms of an A.P., prove that S30=3(S20−S10)
View SolutionIf Sn denotes the sum of the first n terms of an A.P., prove that S30=3(S20−S10)
View SolutionA hemispherical depression is cut out from one face of a cubical block of side 7 cm such that the diameter of the hemisphere is equal to the edge of the cube. Find the surface area of the remaining solid. (Use π=227)
View SolutionIn the given figure, a circle is inscribed in a quadrilateral ABCD in which ∠B=90∘. If AD = 23 cm, AB = 29 cm and DS = 5 cm, find the value of radius (r).
View SolutionFrom a point Q, 13 cm away from the centre of a circle, the length of tangent PQ to the circle is 12 cm. The radius of the circle (in cm) is
View Solutionवृत्त के केंद्र से 13 cm दूर एक बिंदु P हैं। P से वृत्त पर खींची गई स्पर्श रेखा की लम्बाई 12 सेमी हैं| वृत्त की त्रिज्या ज्ञात करें।
View Solutionएक बिंदु P किसी वृत्त के केन्द्र से 13 सेमी की दुरी पर स्थित है । यदि इस बिंदु से वृत्त पर खींची गई स्पर्श रेखा की लम्बाई 12 सेमी हो , तो वृत्त की त्रिज्या ज्ञात कीजिए |
View SolutionFind the length of tangent segment drawn to a circle with radius 5 cm from a point 13 cm from the centre of the circle.
View SolutionFind the length of the tangent from a point 13 cm away from the centre of the circle of radius 5 cm.
View SolutionFrom a point Q ,the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm . The radius of the circle is
View SolutionFrom a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of circle is :
View SolutionFrom a point Q, the length of the tangent to a circle is 12 cm and the distance of Q from the centre is 13 cm. The radius of the circle is 13 cm. The radius of the circle is :
View SolutionFrom a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of circle is :
View SolutionThe length of the tangent drawn to a circle of radius 4 cm from a point 5 cm away from the centre of the circle is
View SolutionThe length of tangent from a point A at a distance of 12 cm from the centre of the circle is 9 cm. What is the radius of the circle ?
View Solution