I. Ltx→0(1+x)2−(1−x)2−2(1+x)3−(1−x)3−3
II. If f(x)=4−7x3x+4andLtx→2f(x)=l,Ltx→0f(x)=m then the equation whose roots are 1/l, 1/m is x2−1=0
only I is true
only II is true
both I and II are true
neither I nor II are true
The correct Answer is:C
Topper's Solved these Questions
- LIMITS AND CONTINUITYBook:DIPTI PUBLICATION ( AP EAMET)Chapter:LIMITS AND CONTINUITYExercise:SET-3Match The Following
Explore 2 Videos
- LIMITS AND CONTINUITYBook:DIPTI PUBLICATION ( AP EAMET)Chapter:LIMITS AND CONTINUITYExercise:Set -4
Explore 8 Videos
- LIMITS AND CONTINUITYBook:DIPTI PUBLICATION ( AP EAMET)Chapter:LIMITS AND CONTINUITYExercise:Exercise 1C(Continuity)
Explore 86 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBook:DIPTI PUBLICATION ( AP EAMET)Chapter:INVERSE TRIGONOMETRIC FUNCTIONSExercise:EXERCISE 2 (SPECIAL TYPE QUESTIONS) (SET - 4)
Explore 5 Videos
- LINEAR PROGRAMMING [APPENDIX-2]Book:DIPTI PUBLICATION ( AP EAMET)Chapter:LINEAR PROGRAMMING [APPENDIX-2]Exercise:Exercise -1
Explore 33 Videos
Similar Questions
Match the following
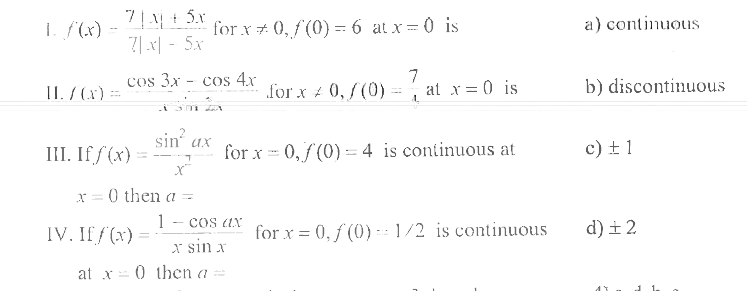
View SolutionAssertion (A) : Ltx→0|x|x=1
Reason (R) : Limit of a function doesn't exist if left and right limits exists and are not equal the correct answer is
View SolutionThe function f(x)=tanx for x≠π/2,f(π/2)=0 at x=π/2 is
View SolutionA : The maximum value of f(x)=Sin−1x+Cos−1x−Tan−1x is 3π/4
R : Sin−1x+Cos−1x=π/2∀x∈R
View SolutionIf 2x+y≥10,x+2y≥10, then the lesat value of F=x+y is
View SolutionIf f(x)=(25−x4)1/4for 0<x<√5,thenf(f(12))=
View SolutionIf f(x)=(25−x4)1/4 for 0<x<√5 then f(f(12))=
View SolutionLtx→−2(1+x)2(1−x)2(1+x)3−(1−x)3=
View SolutionIf f(x)=4−7x3x+4andLtx→2f(x)=m then the equation whose roots are 1, 1/m is
View SolutionLtx→0√1+x2−√1−x+x23x−1=
View SolutionLtx→0(1x+2x+3x+....+nxn)1/x)
View SolutionLtx→01x2=
View SolutionIf f(x)=−√25−x2, then Ltx→1f(x)−f(1)x−1=
View SolutionLtx→0xsin(1x)=
View SolutionA: Ltx→π/2(cotxπ/2−x)=1
R: If Ltx→af(x) exists, then Ltx→af(x)=Ltx→0f(a+x)=Ltx→af(a−x)
View Solution

