If 2x−y+1=0 is a tangent to hyperbola x2a2+y216=1, then which of the following are sides of a right angled triangle ?
2a, 4, 1
2a, 8, 1
a, 4, 1
a, 4, 2
The equations of tangents of slope m to the given hyperbola are
y=mx±√a2m2−16
But, it is given that 2x−y+1=0 or y=2x+1 is tangent to the hyperbla.
∴m=2 and √a2m2−16=1
⇒m=2 and 4a2−16=1
⇒m=2 and a2=174⇒m=2 and a=√172
Clearly, 2a,4,1 are the sides of a triangle as the sum of any two is greater than then third.
टॉपर्स ने हल किए ये सवाल
- HYPERBOLABOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - HYPERBOLAEXERCISE - Section I - Solved Mcqs
54 Videos
- HYPERBOLABOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - HYPERBOLAEXERCISE - Section II - Assertion Reason Type
4 Videos
- FUNCTIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - FUNCTIONSEXERCISE - Chapter Test
29 Videos
- INEQUALITIES BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - INEQUALITIES EXERCISE - EXERCISE SECTION-II (Assertion-Reason )
1 Video
समान प्रश्न
The eccentricity of the conic represented by x2−y2−4x+4y+16=0 is 1 (b) √2 (c) 2 (d) 12
View SolutionStatement-1 : If the foci of a hyperbola are at (4,1) and (−6,1) and eccentricity is 54, then the length of its transverse axis is 4.
Statement-2 : Distance between the foci of a hyperbola is equal to the product of its eccentricity and length of the transverse axis.
View SolutionThe number of bijective functions from set A to itself when A contains 106 elements is
View SolutionIn a triangle ABC , if AB , BC and AC are the three sides of the triangle , then which of the following statements is necessarily true ?
View SolutionIf 2x−y+1=0 is a tangent to the hyperbola x2a2−y216=1 then which of the following CANNOT be sides of a right angled triangle? (a)a,4,2 (b) a,4,1 (c)2a,4,1 (d) 2a,8,1
View SolutionIf 2x−y+1=0 is a tangent to hyperbola x2a2+y216=1, then which of the following are sides of a right angled triangle ?
View SolutionThe area of triangle formed by the lines x−y=0,x+y=0 and any tangent to the hyperbola x2−y2=16 is equal to
View Solutionयदि 2x−y+1=0 अतिपरवलय x2a2−y216=1 की स्पर्शरेखा है तो निम्न में से कौनसी समकोणीय त्रिभुज की भुजायें नहीं हो सकती है (हैं)
View Solutionअतिपरवलय x29−y216=1 तथा y29−x216=1 की उभयनिष्ठ स्पर्श रेखा की प्रवणता है
View SolutionIf 3x+2y−1=0 is a tangent to a hyperbola x216−y29=1, then the point of contact is
View SolutionHyperbola x^2/(25)-y^2/(16)=1 The line that follows 2x+y=1 Is perpendicular to, the equation of is
View SolutionIf 2x−y+1=0 is a tangent to the hyperbola x2a2−y216=1 then which of the following CANNOT be sides of a right angled triangle?
View Solutionआकृति में यदि ABIICD,∠APQ=50∘और∠PRD=127∘ है, तो Y का मान है-
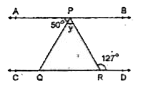
View Solutionयदि 2x−y+1=0 अतिपरवलय x2a2−y216=1 की स्पर्शरेखा है तो निम्न में से कौनसी समकोणीय त्रिभुज की भुजायें नहीं हो सकती है (हैं)
View SolutionTangents drawn from a point on the circle x2+y2=9 to the hyperbola x225−y216=1,
then tangents are at angle
View Solution

