If AD and PM are median of triangles ABC and PQR respectively where ΔABC−ΔPQR, prove that ABPQ=ADPM.Solution in Kannada
The correct Answer is:ABPQ=ADPM
Step by step video, text & image solution for If AD and PM are median of triangles ABC and PQR respectively where Delta ABC - Delta PQR, prove that (AB)/(PQ) = (AD)/(PM). by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Similar Questions
If Adand PM are medians of triangles ABC and PQR, respectively where ΔABC~ΔPQR , prove that ABPQ=ADPM
View SolutionIf AD and PM are medians of triangles ABC and PQR respectively , where ΔABC~ΔPQR, prove that ABPQ=ADPM.
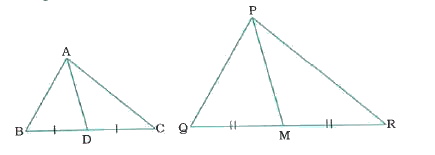
View SolutionSides AB and AC and median AD of a triangle ABC are proportional to sides PQ and PR and median PM of another triangle PQR. Prove that △ABC−△PQR .
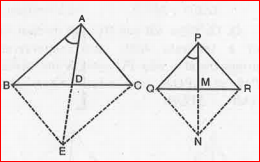 .
.
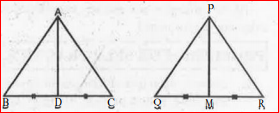
View SolutionIf AD and PM are medians of triangles ABC and PQR, respectively where △ABC~△PQR , Prove that ABPQ=ADPM .
 .
.
View Solutionਇੱਕ ਤ੍ਰਿਭੁਜ ABC ਦੀਆਂ ਕ੍ਰਮਵਾਰ ਭੁਜਾਵਾਂ AB ਅਤੇ BC ਮੱਧਿਕਾ AD ਕਿਸੇ ਹੋਰ ਤ੍ਰਿਭੁਜ PQR ਦੀਆਂ ਕ੍ਰਮਵਾਰ ਭੁਜਾਵਾਂ PQ,QR ਅਤੇ ਮੱਧਿਕਾ PM ਦੇ ਸਮਾਨ-ਅਨੁਪਾਤੀ ਹਨ(ਦੇਖੋ ਚਿੱਤਰ 6.41)।ਦਿਖਾਉ ਕਿ ΔABC~ΔPQR ਹੈ।
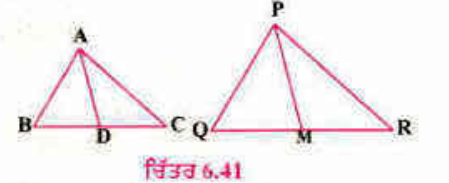
View SolutionAD ਅਤੇ PM ਤ੍ਰਿਭੁਜਾਂ ABC ਅਤੇ PQR ਦੀਆਂ ਕ੍ਰਮਵਾਰ ਮੱਧਿਕਾਵਾਂ ਹਨ, ਜਦੋਂ ਕਿ ΔABC~ΔPQR ਹੈ।ਸਿੱਧ ਕਰੋ ਕਿ ABPQ=ADPM ਹੈ।
View SolutionIf AD and PM are medians of triangles ABC and PQR,respectively where △ABC~△PQR,prove thatABPQ=ADPM.
View Solution
