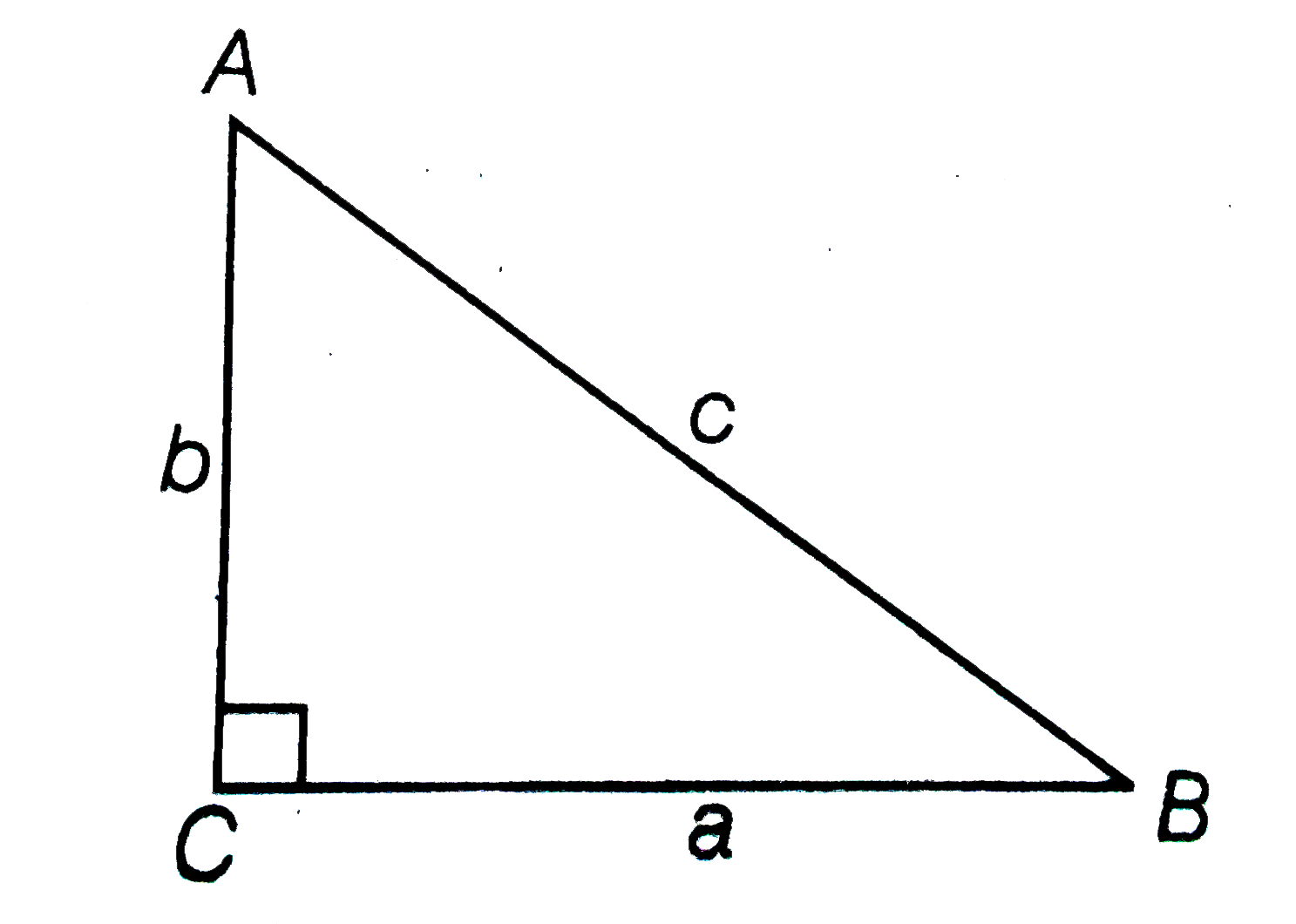
If ΔABC is a right angled at C, then tan A + tan B is equal to
A
b2ac
B
a+b
C
a2bc
D
c2ab
Video Solution
Text Solution
The correct Answer is:D
Clearly , tanA=ab,tanB=ba
Now tanA+tanB=a2+b2ab
a2+b2=c2
tanA+tanB=c2ab
|
Topper's Solved these Questions
- TRIGONOMETRIC FUNCTIONS Book:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:TRIGONOMETRIC FUNCTIONS Exercise:EXERCISE 2 (MISCELLANEOUS PROBLEMS)
Explore 26 Videos
- TRIGONOMETRIC FUNCTIONS Book:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:TRIGONOMETRIC FUNCTIONS Exercise:EXERCISE 2 (MISCELLANEOUS PROBLEMS)
Explore 26 Videos
- THREE DIMENSIONAL GEOMETRYBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:THREE DIMENSIONAL GEOMETRYExercise:MHT CET Corner
Explore 3 Videos
- TRIGONOMETRIC FUNCTIONS OF COMPOUND ANGLESBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:TRIGONOMETRIC FUNCTIONS OF COMPOUND ANGLESExercise:Exercise 2 (MISCELLANEOUS PROBLEMS)
Explore 20 Videos
Similar Questions
Knowledge Check
If ΔABC is right angled at C, then the value of cos(A+B) is
A0B1C12D√32In a triangle ABC, right angled at C, find the value of tan A + tan B in terms of the sides a,b,c.
Aa2bcBa+bCb2acDc2abIn ΔABC right angled at B, If tanA=√3, then cosAcosC−sinAsinC =
A−1B0C1D√32
if in triangle ABC right angled at C then tanA+tanB
View SolutionIn a triangle ABC, right angled at C,tanA+tanB is equal to a+b b. c2ab c. a2bc d. b2ac
View SolutionIf ΔABC is right-angled at C, then c−c.sinAtan(A2)=....
View SolutionIn a triangle ABC, right angled at C, find the value of tan A + tan B in terms of the sides a,b,c.
View SolutionIn ΔABC right angled at B, if tan A=√3, then cos A cos C- sin A sin C =
View Solution
