If from an extrenal point B of a circle with centre 0, two tangents BC and BD are drawn such that ∠DBC=120∘, prove that BC+BD=BO i.e., BO=2BC.
Step by step video solution for If from an extrenal point B of a circle with centre 0, two tangents BC and BD are drawn such that angleDBC=120^(@), prove that BC+BD=BO i.e., BO=2BC. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Similar Questions
O केन्द्र के वृत्त में, यदि एक बाह्य बिन्दु B से दो स्पर्श रेखाएँ BC और BD इस प्रकार खींची जाती है कि ∠DBC=120∘ है , तो सिद्ध कीजिए कि BC+BD=BO.
View Solutionसिद्ध कीजिए कि: ∣∣∣ad+bcac−bdbd−acad+bc∣∣∣=(a2+b2)(c2+d2)
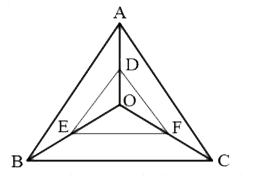
View SolutionIn the figure, a point O inside △ABC is joined to its vertices. From a point D on AO, DE is drawn parallel to AB and from a point E on BO, EF is drawn parallel to BC. Prove that DF || AC.
View SolutionIf from an extrenal point B of a circle with centre 0, two tangents BC and BD are drawn such that ∠DBC=120∘, prove that BC+BD=BO i.e., BO=2BC.
View SolutionIn the figure, O is the center of the circle and BO is the bisector of ∠ABC show that AB=BC
View SolutionIf BD is the perpendicular drawn from the vertex B of the right triangle ABC to the hypotenuse AC,prove that(iii)BC2=CD×AC
View SolutionAB and BD are two parallel sides of trapezium ABCD. if the diagonals AC and BD meet at O, then prove that (AO)/(OC) = (BO)/(OD) .
View SolutionIf from an external point B of a circle with centre O, two tangents BC and BD are drawn such that ∠DBC=120∘, prove that BC+BD=BO.
View Solution