If f(x)=xx−1, then prove that f(a)f(a+1)=f(a2)
The correct Answer is:f(a2)
To prove that f(a)f(a+1)=f(a2) for the function f(x)=xx−1, we will follow these steps:
Step 1: Calculate f(a)
We start by substituting a into the function f(x):
f(a)=aa−1
Step 2: Calculate f(a+1)
Next, we substitute a+1 into the function:
f(a+1)=a+1(a+1)−1=a+1a
Step 3: Calculate f(a)f(a+1)
Now we will find the ratio f(a)f(a+1):
f(a)f(a+1)=aa−1a+1a=aa−1⋅aa+1
This simplifies to:
a2(a−1)(a+1)
Step 4: Simplify the expression
We can recognize that (a−1)(a+1)=a2−1. Thus, we have:
f(a)f(a+1)=a2a2−1
Step 5: Calculate f(a2)
Now we will calculate f(a2):
f(a2)=a2a2−1
Step 6: Compare the two expressions
Now we can compare f(a)f(a+1) and f(a2):
f(a)f(a+1)=a2a2−1=f(a2)
Conclusion
Thus, we have shown that:
f(a)f(a+1)=f(a2)
This completes the proof.
---
टॉपर्स ने हल किए ये सवाल
- RELATIONS AND FUNCTIONSBook:ICSEChapter:RELATIONS AND FUNCTIONSExercise:EXERCISE 2 (a)
Explore 24 Videos
- RELATIONS AND FUNCTIONSBook:ICSEChapter:RELATIONS AND FUNCTIONSExercise:EXERCISE 2 (b)
Explore 26 Videos
- RELATION AND FUNCTIONSBook:ICSEChapter:RELATION AND FUNCTIONSExercise:MULTIPLE CHOICE QUESTIONS (Choose the correct answer from the given four options in questions)
Explore 32 Videos
- SAMPLE QUESTION PAPER 01Book:ICSEChapter:SAMPLE QUESTION PAPER 01Exercise:SECTION C
Explore 8 Videos
समान प्रश्न
x∈{2,4,6,9} and y∈{4,6,18,27,54}. Form all ordered pairs (x,y) such that x is factor of y and x≤y.
View SolutionWrite down the relation shown by the arrow diagram, by listing the ordered pairs. State the domain, co-domain, and the range of the relation.
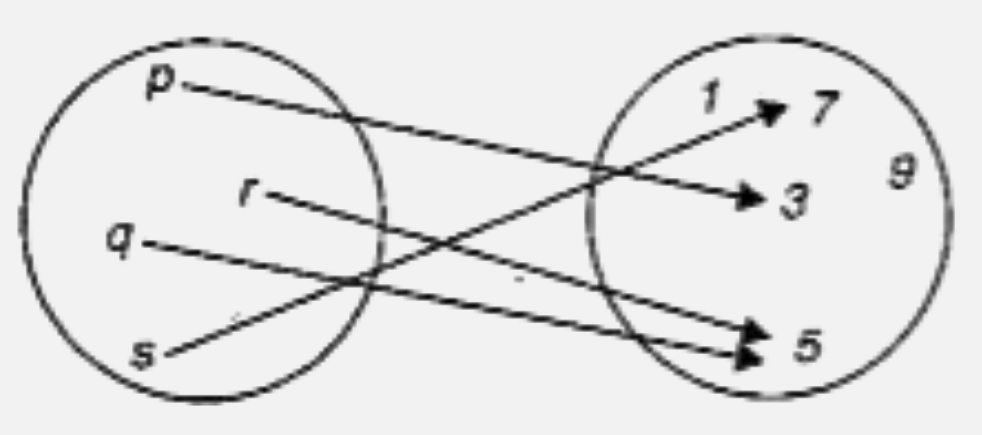
View SolutionIf A = (-1,2,5,8), B = {0,1,3,6,7) and R be the relation "is one less than" from A to B, then R as a set of ordered pairs is
View SolutionThe price index of a commodity is 140. Then, the percentage increase in price of the commodity in current year as compared to the base year is :
View SolutionIf f'(x)>0,f(x)>0AA x in(0,1) and f(0)=0,f(1)=1, then prove that 'f(x)f^(^^)-1(x)
View Solutionf(x)=(ax^(2)+1)/(x^(2)+1),lim_(x rarr0)f(x)=1 and lim_(x rarr oo)f(x)=1, then prove that f(-2)=f(2)=1
View SolutionIf f(x)=x+1x, then prove that :
{f(x)}3=f(x3)+3⋅f(1x)
View Solutionयदि f(x)=log(1+x1−x), तो साबित करें कि
f,(2x1+x2)=2f(x)
View Solutionयदि f(x)=1+x1−x.
तो साबित कीजिए कि f(x).f(x2)1+[f(x)]2=12
View Solutionयदि f(x)=1x तो सिद्ध कीजिए कि limh→0f(x+h)−f(x)h=−1x2
View Solutionयदि f(x)=x+1x, तो सिद्ध कीजिए कि {f(x)}3=f(x3)+3⋅f(1x)
View Solutionयदि f(x)=x2−1x2+1, तो सिद्ध कीजिए -
f(x)+f(1x)=0.
View SolutionIf f(x)=x−1x+1, then prove that f(x)−f(y)1+f(x)f(y)=x−y1+xy.
View SolutionIf f(x)=1−x1+x, prove that
f{f(1x)}=1x[x≠0]
View SolutionIf f(x)=1−x1+x, prove that
f[f{f(1x)}]=−f(x)
View Solution
