If in a rectangle ABCD, diagonal AC bisect ∠A as well as ∠C then ABCD is a
Parallelogram
square
Rhombus
Trapezium
The correct Answer is:C
To solve the problem, we need to prove that if in rectangle ABCD, diagonal AC bisects both angle A and angle C, then ABCD is a square.
1. Understanding the Properties of a Rectangle:
- A rectangle has opposite sides that are equal and all angles are 90 degrees.
2. Given Information:
- Diagonal AC bisects angle A and angle C.
- This means that angle A is divided into two equal angles, and angle C is also divided into two equal angles.
3. Setting Up the Angles:
- Let angle A = 2α (since it is bisected, each part will be α).
- Similarly, let angle C = 2β (since it is bisected, each part will be β).
4. Using the Properties of a Rectangle:
- In a rectangle, angle A and angle C are both 90 degrees.
- Therefore, we can set up the equations:
- 2α = 90 degrees → α = 45 degrees
- 2β = 90 degrees → β = 45 degrees
5. Analyzing the Triangle Formed by the Diagonal:
- Consider triangle ABC formed by points A, B, and C.
- Since angle A = 45 degrees and angle B = 90 degrees, angle C must also be 45 degrees (because the sum of angles in a triangle is 180 degrees).
6. Using the Isosceles Triangle Property:
- In triangle ABC, since angle A = angle C = 45 degrees, it follows that sides AB and BC must be equal (because the angles opposite to equal sides are equal).
7. Conclusion About the Sides:
- Since AB = BC and also AD = DC (as opposite sides of a rectangle are equal), we can conclude that all sides of rectangle ABCD are equal (AB = BC = CD = DA).
8. Final Conclusion:
- Since all sides are equal and all angles are 90 degrees, rectangle ABCD is a square.
Final Answer:
ABCD is a square.
---
- A rectangle has opposite sides that are equal and all angles are 90 degrees.
- Diagonal AC bisects angle A and angle C.
- This means that angle A is divided into two equal angles, and angle C is also divided into two equal angles.
- Let angle A = 2α (since it is bisected, each part will be α).
- Similarly, let angle C = 2β (since it is bisected, each part will be β).
- In a rectangle, angle A and angle C are both 90 degrees.
- Therefore, we can set up the equations:
- 2α = 90 degrees → α = 45 degrees
- 2β = 90 degrees → β = 45 degrees
- Consider triangle ABC formed by points A, B, and C.
- Since angle A = 45 degrees and angle B = 90 degrees, angle C must also be 45 degrees (because the sum of angles in a triangle is 180 degrees).
- In triangle ABC, since angle A = angle C = 45 degrees, it follows that sides AB and BC must be equal (because the angles opposite to equal sides are equal).
- Since AB = BC and also AD = DC (as opposite sides of a rectangle are equal), we can conclude that all sides of rectangle ABCD are equal (AB = BC = CD = DA).
- Since all sides are equal and all angles are 90 degrees, rectangle ABCD is a square.
ABCD is a square.
Topper's Solved these Questions
- QUARILATERAL Book:CBSE COMPLEMENTARY MATERIALChapter:QUARILATERAL Exercise:PART-A( True (T) and False (F))
Explore 6 Videos
- QUARILATERAL Book:CBSE COMPLEMENTARY MATERIALChapter:QUARILATERAL Exercise:Part - B
Explore 12 Videos
- PROBABILITY MIND MAPBook:CBSE COMPLEMENTARY MATERIALChapter:PROBABILITY MIND MAPExercise:PRACTICE TEST
Explore 6 Videos
- STATISTICSBook:CBSE COMPLEMENTARY MATERIALChapter:STATISTICSExercise:PRACTICE TEST
Explore 5 Videos
Similar Questions
In a parallelogram, the diagonals are equal ( T / F )
View SolutionTheorem 1 the sum of the angles of a quadrilateral is 360∘ or 4 right angles.
View SolutionWrite the probability of an impossible event.
View SolutionWrite class size and class limits of the following:
47,52,57,62,67,72,77
View SolutionABCD is a rectangle in which diagonal AC bisects ∠Aas well as ∠C. Show that:
(i) ABCD is a square
(ii) diagonal BD bisects ∠Bas well as ∠D..
View SolutionDiagonal AC of a paraleligram ABCD bisects ∠A (sec figure). Show that:
(i) it bisects ∠C also (ii) ABCD is a rhombus.
View SolutionABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that
(i) ABCD is a square
(ii) diagonal AD bisects ∠B
View Solutionएक समान्तर चतुर्भुर्ज ABCD व विकर्ण AC,∠A को समद्विभाजित करता है तो सिद्ध कीजिए की-
(i) यह ∠C को भी समद्विभाजित करता है
(ii) का समचतुर्भुर्ज है।
View SolutionDiagonals AC of a parallelogram ABCD bisects ∠A. Show that
it bisects ∠C also
ABCD is a rhombus
View SolutionABCD is a rhombus Show that diagonal AC bisects ∠A as well as ∠C and diagonal BD bisects ∠B as well as ∠D.
View SolutionABCD is a rectangle in which diagonals AC bisects ∠A as well as ∠C, Show that
ABCD is a square
diagonal BD bisects ∠B as well as ∠D
View SolutionDiagonal AC of a parallelogram ABCD bisects ∠A. Show that
(i) it bisects ∠C alo (ii) ABCD is a rhombus.

View SolutionABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C . Show that: (i) ABCD is a square (ii) diagonal BD bisects ∠B as well as ∠D. .
View SolutionABCD is a rectangle in which diagonal AC bisects ∠Aas well as ∠C. Show that:(i) ABCD is a square (ii) diagonal BD bisects ∠Bas well as ∠D..
View SolutionIf in rectangle ABCD
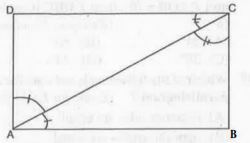 , diagonal AC bisects ∠A as well as ∠C , then ABCD is a :
, diagonal AC bisects ∠A as well as ∠C , then ABCD is a :
View Solution