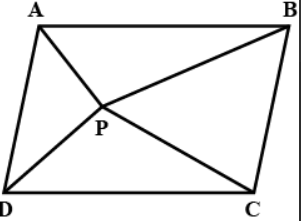
If P is any point in the interior of a parallelogram ABCD , then prove that area of the triangle APB is less than half the are of parallelogram.
Step by step video solution for If P is any point in the interior of a parallelogram A B C D , then prove that area of the triangle A P B is less than half the are of parallelogram. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLESBook:MTG IIT JEE FOUNDATIONChapter:AREAS OF PARALLELOGRAMS AND TRIANGLESExercise:EXERCISE ( Subjective Problems ) (Short Answer Type )
Explore 4 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBook:MTG IIT JEE FOUNDATIONChapter:AREAS OF PARALLELOGRAMS AND TRIANGLESExercise:EXERCISE ( Subjective Problems ) (Long Answer Type )
Explore 3 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBook:MTG IIT JEE FOUNDATIONChapter:AREAS OF PARALLELOGRAMS AND TRIANGLESExercise:EXERCISE ( Comprehension Type )
Explore 6 Videos
- CIRCLES Book:MTG IIT JEE FOUNDATIONChapter:CIRCLES Exercise:OLYMPIAD/HOTS CORNER
Explore 6 Videos
Similar Questions
In Δ ABC, D is the mid-point of AB and P is any point on BC. If CQ∣∣PD meets AB and Q (shown in figure), then prove that
ar(ΔBPQ)=12ar(ΔABC).

View SolutionABCD is a parallelogram. X and Y are mid-points of BC and CD. Prove that ar(△AXY)=38ar(∣∣gmABCD)
View SolutionABCD is a trapezium in which AB || DC a and DC= 40 cm and AB = 60 cm. If X and Y a re respectively, the midpoints of AD and BC, then

XY=
View SolutionABCD is a cyclic quadrilateral, if ∠BAC=60∘,∠BCA=20∘, then find the value of ∠ADC.
View SolutionIn Figure, ABC is an isosceles triangle in which AB=AC.CPparel≤lAB and AP is the bisector of exterior ∠CAD of ABC . Prove that ∠PAC=∠BCA and (ii) ABCP is a parallelogram.

View SolutionIf P is any point in the interior of a parallelogram ABCD , then prove that area of the triangle APB is less than half the are of parallelogram.
View SolutionIn Figure, P is a point in the interior of a parallelogram ABCD . Show that ar(APB)+ar(PCD)=12ar(^(gm)ABCD) aR(APD)+ar(PBC)=ar(APB)+ar(PCD)
View SolutionABCD is a parallelogram. P is a point on AD such that AP=13 AD and Q is a point on BC such that: CQ=13BC. Prove that AQCP is a parallelogram.
View SolutionIn Figure, P is a point in the interior of a parallelogram ABCD. Show that ar(APB)+ar(PCD)=12ar (||gmABCD) ar (APD)+ar (PBC)=ar (APB)+ar(PCD)

View SolutionIf P is any point in the interior of a parallelogram ABCD, then prove that area of the triangle APB is less than half the area of parallelogram.
View SolutionABCD is a parallelogram whose diagonals intersect at O. If P is any point on BO, prove that: ar (ADO)=AR (CDO) ar ( ABP)= ar ( CBP)
View Solutionयदि किसी चतुर्भुज ABCD के अन्तः क्षेत्र में स्थित कोई बिंदु P है तो सिद्ध कीजिए कि ΔAPB का क्षेत्रफल समांतर चतुर्भुज के क्षेत्रफल के आधे से कम होता है।
View SolutionP is any point in the interior of the parallelogram ABCD. Prove that ΔAPD+ΔBPC = 12 parallelogram ABCD.
View SolutionIn Figure, ABC is an isosceles triangle in which AB=AC.andCP∣∣AB and AP is the bisector of exterior ∠CAD of ABC . Prove that ∠PAC=∠BCA and (ii) ABCP is a parallelogram.
View SolutionABCD is a parallelogram. P is a point on AD such that AP=13AD and Q is a point on BC such that CQ=13BP . Prove that AQCP is a parallelogram.
View SolutionIf P is any point in the interior of a parallelogram ABCD , then prove that area of the triangle APB is less than half the are of parallelogram.
View Solution