If set A ={x∣x2(x−5)(2x−1)(5x+1)(x+2)<0} and
Set B={x∣3x+16x3+x2−x>0} then A∩B does not contain
(a) (1,4)
(b) (5,11)
(c)
(−32,−12)
(d) None of theseSolution in Bengali
(1,4)
(5,11)
(−32,−12)
None of these
The correct Answer is:B
we have x2(x−5)(2x−1)(5x+1)(x+2)<0 ltbgt 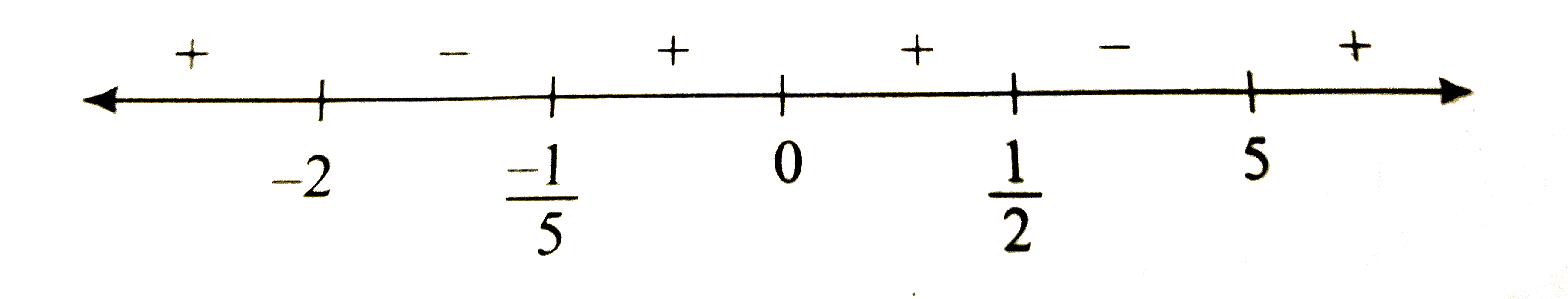
from the sign scheme , solution is (−2,−15)∪(15,5)
Now 3x+16x3+x2−x>0
⇒3x+1x(3x−1)(2x+1)>0
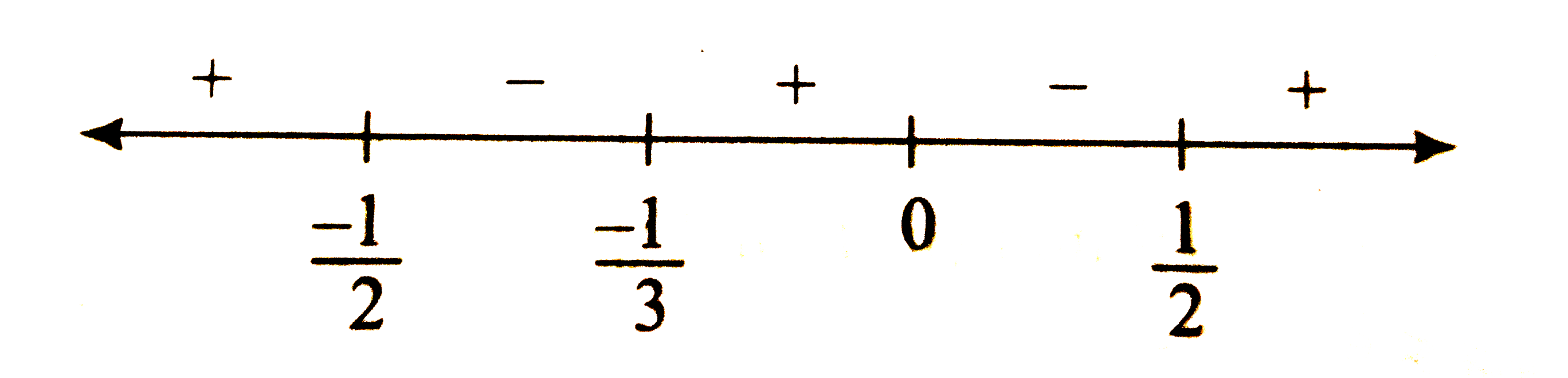
form the sign scheme solution is
(−∞,−12)∪(−13,0)∪(13,∞)
Clearly from (i) and (ii) options ( s) (1) and ( 3) and correct
Topper's Solved these Questions
- SET THEORY AND REAL NUMBER SYSTEM BOOK - CENGAGE PUBLICATIONCHAPTER - SET THEORY AND REAL NUMBER SYSTEM EXERCISE - Archives
1 Video
- SET THEORY AND REAL NUMBER SYSTEM BOOK - CENGAGE PUBLICATIONCHAPTER - SET THEORY AND REAL NUMBER SYSTEM EXERCISE - Concept Application Exercise 1.5
12 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - All Questions
1119 Videos
- SOLUTIONS AND PROPERTIES OF TRIANGLE BOOK - CENGAGE PUBLICATIONCHAPTER - SOLUTIONS AND PROPERTIES OF TRIANGLE EXERCISE - Comprehension Type
6 Videos
Similar Questions
If A,B and C are three sets such that A∩B=A∩CandA∪B=A∪C then
View SolutionIf ∣∣x2−7∣∣≤9 then find the values of x
View SolutionIf the function f:[1,∞)→[1,∞) is defined by f(x)=2x(x−1), then find f−1(x)
View SolutionLet ABC be a triangle in which the line joining the circumecentre and incentre is parallel to base BC of the triangle. Then answer the following questions :
Then range of ∠A is
View SolutionIf (x)=∣∣x2+4x−32x+4132x2+5x−94x+5268x2−6x+116x−6104∣∣=ax3+bx2+cx+d, then a=3 b. b=0 c.c=0 d. none of these
View SolutionIf S is the set of all real 'x' such that (x^2(5-x)(1-2x))/((5x+1)(x+2)) is negative and (3x+1)/(6x^3+x^2-x) is positive, then S contains
View SolutionIf set A ={x∣x2(x−5)(2x−1)(5x+1)(x+2)<0} and
Set B={x∣3x+16x3+x2−x>0} then A∩B does not contain
View SolutionLet Z be the set of integers. If A = {x∈Z:2(x+2)(x2−5x+6)=1 and B={x∈Z:−3<2x−1<9}, then the number of subsets of the set A × B is
View SolutionLet Z be the set of integers. If
A={x∈Z:2(x+2)(x2−5x+6)=1}
and B={x∈Z:−3<2x−1<9}, then the number of subsets of the set A×B, is
View SolutionIf (x)=∣∣[x2+4x−32x+413][2x2+5x−94x+526][8x2−6x+116x−6104]∣∣=ax3+bx2+cx+d, then a=3 b. b=0 c.c=0 d. none of these
View SolutionIf set A ={x∣x2(x−5)(2x−1)(5x+1)(x+2)<0} and
Set B={x∣3x+16x3+x2−x>0} then A∩B does not contain
View SolutionLet Z be the set of integers. If A = {x∈Z:2(x+2)(x2−5x+6)=1 and B={x∈Z:−3<2x−1<9}, then the number of subsets of the set A × B is
View Solutionनिम्न के लिए x का परिसर ज्ञात कीजिए
(a) (x−2)(x+3)≥0 (b)xx+1>2
(c)3x−14x+1≤0 (d)(2x−1)(x+3)(2−x)(1−x)2x4(x+6)(x−9)(2x2+4x+9)<0
(e) 7x−17x2−3x+4≥1 (f)x2+2≤3x≤2x2−5
View SolutionIf (x)= |x^2+4x-3 2x+4 13 2x^2+5x-9 4x+5 26 8x^2-6x+1 16 x-6 104|=a x^3+b x^2+c x+d ,thena=3b.b=0c.c=0 d. none of these
View SolutionIf set A ={x∣x2(x−5)(2x−1)(5x+1)(x+2)<0} and
Set B={x∣3x+16x3+x2−x>0} then A∩B does not contain
View Solution

