If the 7thand10th term of an AP are 18 and −6 respectively , which term of the AP is zero ?
To solve the problem step by step, we need to find the first term (A) and the common difference (D) of the arithmetic progression (AP) using the information given about the 7th and 10th terms.
Step 1: Write the formulas for the 7th and 10th terms of the AP.
The nth term of an AP can be expressed as:
Tn=A+(n−1)D
Where:
- Tn is the nth term
- A is the first term
- D is the common difference
- n is the term number
For the 7th term:
T7=A+(7−1)D=A+6D
Given that T7=18:
A+6D=18(1)
For the 10th term:
T10=A+(10−1)D=A+9D
Given that T10=−6:
A+9D=−6(2)
Step 2: Solve the equations simultaneously.
Now we have two equations:
1. A+6D=18 (equation 1)
2. A+9D=−6 (equation 2)
We can subtract equation (1) from equation (2):
(A+9D)−(A+6D)=−6−18
This simplifies to:
3D=−24
Now, divide both sides by 3:
D=−8
Step 3: Substitute D back into one of the equations to find A.
Now that we have D, we can substitute it back into equation (1):
A+6(−8)=18
This simplifies to:
A−48=18
Adding 48 to both sides gives:
A=66
Step 4: Find the term of the AP that is zero.
We need to find n such that:
Tn=A+(n−1)D=0
Substituting A and D:
66+(n−1)(−8)=0
This simplifies to:
66−8(n−1)=0
Expanding gives:
66−8n+8=0
Combining like terms:
74−8n=0
Now, solving for n:
8n=74
n=748=374
Conclusion
Since n=374 is not an integer, it means there is no term in this AP that is exactly zero.
The nth term of an AP can be expressed as:
Tn=A+(n−1)D
Where:
- Tn is the nth term
- A is the first term
- D is the common difference
- n is the term number
T7=A+(7−1)D=A+6D
Given that T7=18:
A+6D=18(1)
T10=A+(10−1)D=A+9D
Given that T10=−6:
A+9D=−6(2)
Now we have two equations:
1. A+6D=18 (equation 1)
2. A+9D=−6 (equation 2)
(A+9D)−(A+6D)=−6−18
This simplifies to:
3D=−24
Now, divide both sides by 3:
D=−8
Now that we have D, we can substitute it back into equation (1):
A+6(−8)=18
This simplifies to:
A−48=18
Adding 48 to both sides gives:
A=66
We need to find n such that:
Tn=A+(n−1)D=0
Substituting A and D:
66+(n−1)(−8)=0
This simplifies to:
66−8(n−1)=0
Expanding gives:
66−8n+8=0
Combining like terms:
74−8n=0
Now, solving for n:
8n=74
n=748=374
Since n=374 is not an integer, it means there is no term in this AP that is exactly zero.
Topper's Solved these Questions
- DIKSHA QUESTIONS Book:OSWAL PUBLICATIONChapter:DIKSHA QUESTIONS Exercise:Unit -II : Algebra (Arithmetic Progressions) (Long Answer Type Questions )
Explore 11 Videos
- DIKSHA QUESTIONS Book:OSWAL PUBLICATIONChapter:DIKSHA QUESTIONS Exercise:Unit -III: Coordinate Geometry (Coordinate Geometry ) (Multiple Choice Questions)
Explore 5 Videos
- DIKSHA QUESTIONS Book:OSWAL PUBLICATIONChapter:DIKSHA QUESTIONS Exercise:Unit -II : Algebra (Arithmetic Progressions) (Very Short Answer type Questions )
Explore 8 Videos
- COORDINATE GEOMETRYBook:OSWAL PUBLICATIONChapter:COORDINATE GEOMETRYExercise:SELF ASSESSMENT
Explore 20 Videos
- INTRODUCTION TO TRIGONOMETRY Book:OSWAL PUBLICATIONChapter:INTRODUCTION TO TRIGONOMETRY Exercise:Self - Assessment
Explore 15 Videos
Similar Questions
If the sum of n terms of an A.P. is 3n2+5n and its mth term is 164, find the value of m.
View SolutionIn the given figure, MN∣∣AB,BC=7.5cm,AM=4cmandMC=2cm. Find the length of BN.
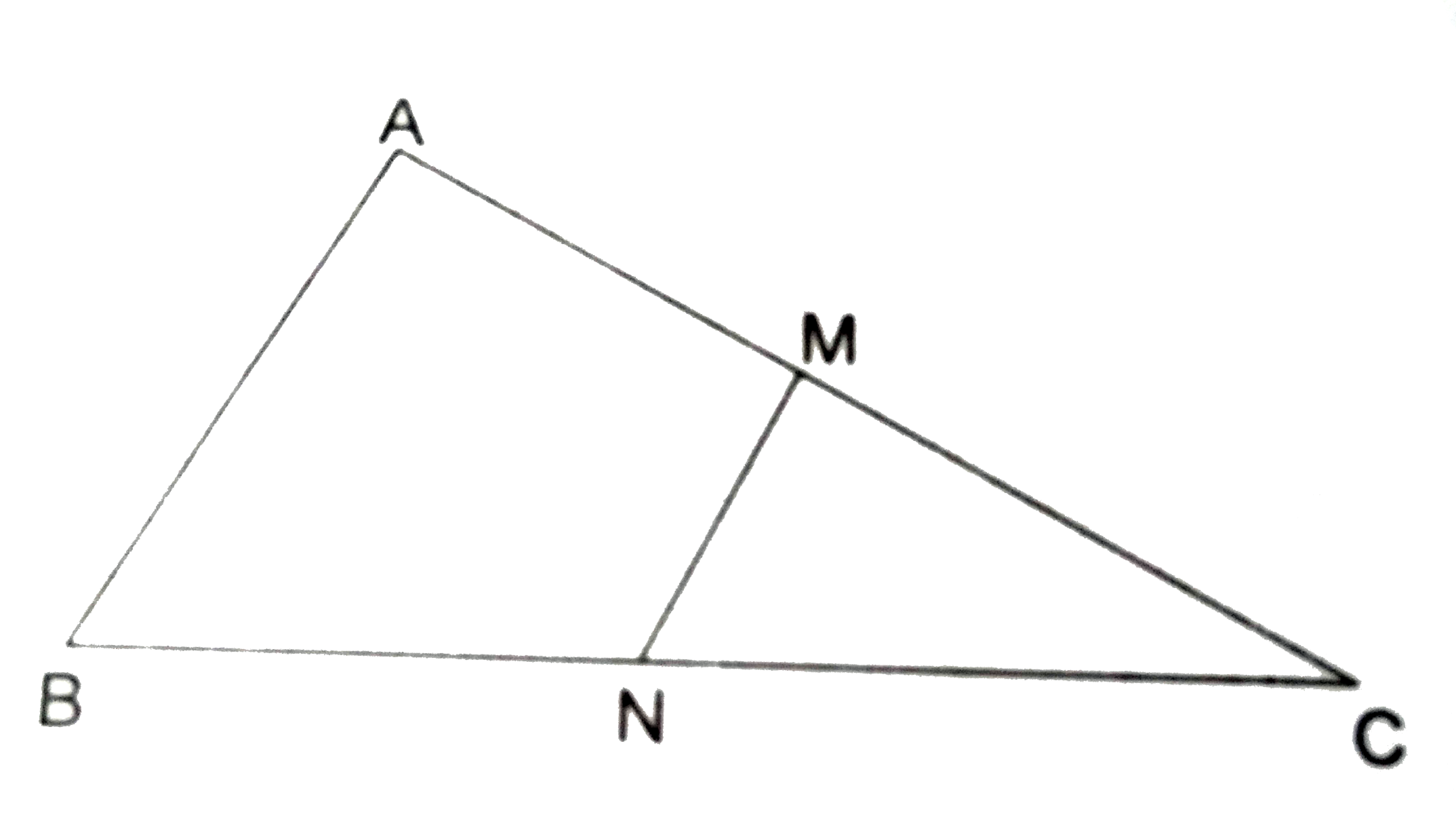
View SolutionFind the first term and the common difference 13,53,93,133…….
View SolutionFind the point on the X -axis which is equidistant from the points A(2,−5)andB(−2,9)
View SolutionIn ΔABC right - angled at c, AB = 29 units BC = 21 units and ∠ABC=θ Determine the value of
cos2θ+sin2θand
View SolutionThe sum of the 4th and 8th terms of an AP is 24 and the sum of the 6th and 10th terms is 44. Find the first three terms of the AP.
View SolutionIf the 3rd and the 9thterms of an AP are 4 and −8 respectively, which term of this AP is zero?
View SolutionIf 7 xx the 7 th term of an AP is equal to 11 xx its 11 th term,show that the 18 th term of the AP is 0.
View SolutionThe sum of the 4^(th) and 8^(th) terms of an AP is 24 and the sum of its 6^(th) term and 10^(th) term is 44. Find the first three terms of the AP.
View SolutionIf the 10^(th) term of an AP is 52 and 17^(th) term is 20 more than its 13^(th) term.Find the AP.
View SolutionIf the 8th term of an AP is 31 and the 15th term of an AP is 16 more than the 11th term . find the AP.
View SolutionThe 6 th term of an AP is 20 and its 11 th term is 35. Find the 25 th term of the AP.
View SolutionIf the 5th term and the 14 th term of an AP are 35 and 8 respectively, then find the 20 th term of the AP.
View SolutionThe sum of the 4th and 8th terms of an AP is 24 and the sum of the 6th and 10th terms is 44. find the first three terms of the AP.
View SolutionThe 10th term of the AP 3,11,19,…. Is ……….
View SolutionIf the 3rd and the 9th terms of an AP are 4 and -8 respectively, which term of this AP is zero ?
View Solution