If the angles of a triangle are in the ratio 3:4:5, then the triangle formed will be
Right angled triangle
Isosceles triangle
Scalene triangle
Obtuse angled triangle
The correct Answer is:C
To determine the type of triangle formed by the angles in the ratio 3:4:5, we can follow these steps:
1. Understand the Ratio of Angles:
The angles of the triangle are given in the ratio of 3:4:5. This means we can express the angles as:
- Angle A = 3x
- Angle B = 4x
- Angle C = 5x
2. Use the Triangle Angle Sum Property:
The sum of the angles in any triangle is always 180 degrees. Therefore, we can set up the equation:
3x+4x+5x=180
3. Combine Like Terms:
Combine the terms on the left side of the equation:
12x=180
4. Solve for x:
To find the value of x, divide both sides of the equation by 12:
x=18012=15
5. Calculate Each Angle:
Now that we have the value of x, we can find each angle:
- Angle A = 3x = 3(15) = 45 degrees
- Angle B = 4x = 4(15) = 60 degrees
- Angle C = 5x = 5(15) = 75 degrees
6. Identify the Type of Triangle:
Now we have the angles: 45 degrees, 60 degrees, and 75 degrees.
- Since all angles are less than 90 degrees, this triangle is not a right triangle.
- Since all angles are different, it is not an isosceles triangle.
- Since all angles are less than 90 degrees, it is not an obtuse triangle.
- Therefore, the triangle is classified as an acute triangle.
Conclusion:
The triangle formed by the angles in the ratio 3:4:5 is an acute triangle.
The angles of the triangle are given in the ratio of 3:4:5. This means we can express the angles as:
- Angle A = 3x
- Angle B = 4x
- Angle C = 5x
The sum of the angles in any triangle is always 180 degrees. Therefore, we can set up the equation:
3x+4x+5x=180
Combine the terms on the left side of the equation:
12x=180
To find the value of x, divide both sides of the equation by 12:
x=18012=15
Now that we have the value of x, we can find each angle:
- Angle A = 3x = 3(15) = 45 degrees
- Angle B = 4x = 4(15) = 60 degrees
- Angle C = 5x = 5(15) = 75 degrees
Now we have the angles: 45 degrees, 60 degrees, and 75 degrees.
- Since all angles are less than 90 degrees, this triangle is not a right triangle.
- Since all angles are different, it is not an isosceles triangle.
- Since all angles are less than 90 degrees, it is not an obtuse triangle.
- Therefore, the triangle is classified as an acute triangle.
The triangle formed by the angles in the ratio 3:4:5 is an acute triangle.
टॉपर्स ने हल किए ये सवाल
- LINES AND ANGLESBook:SCIENCE OLYMPIAD FOUNDATION Chapter:LINES AND ANGLESExercise:Achievers Section (HOTS)
Explore 3 Videos
- LINEAR EQUATIONS IN TWO VARIABLES Book:SCIENCE OLYMPIAD FOUNDATION Chapter:LINEAR EQUATIONS IN TWO VARIABLES Exercise:ACHIEVERS SECTION (HOTS)
Explore 2 Videos
- LOGICAL REASONING Book:SCIENCE OLYMPIAD FOUNDATION Chapter:LOGICAL REASONING Exercise:NON-VERBAL REASONING
Explore 9 Videos
समान प्रश्न
Fill in the blanks
(a) Angles forming a linear pair are ____(P) angles.
(b) The angle between the bisectors of the two acute angles of a right-angled triangle is of measure ____(Q)
(c ) Sum of interior angles of a quadrilateral is ____(R)
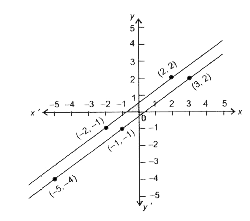
View SolutionThe equation representing the given graph is ______.
View SolutionWhich of the following figures will continue the same series as established by the Problem Figures ?

View SolutionThe angles of a triangle are in the ratio 3:4:5. Find the smallest angle.
View SolutionThe angles of a triangle are in the ratio 3:5:7. The triangle is
View Solutionयदि एक त्रिभुज के कोण 3:4:5 के अनुपात में है तब छोटा कोण है -
View Solutionयदि किसी त्रिभुज के कोणों में 3:4:5 का अनुपात है, तो उनकी भुजाओ में अनुपात ज्ञात कीजिए ।
View SolutionIf the angles of a triangle are in the ratio 3:4:5,then the sides are in the ratio
View SolutionIf the angles of a triangle are in the ratio 3:4:5, then the sides are in the ratio
View SolutionIf the ratio of the angles of a triangle 3:4:5 If, then find all its angles.
View SolutionThe angles of a triangle are in the ratio 3:4:5. Find the smallest angle.
View SolutionRatio of 3 angles of a triangle are 3:4:5. Find each angle.
View Solutionयदि किसी त्रिभुज की कोणों में अनुपात 3:4:5 हो, तो कोणों को ज्ञात किजिए।
View SolutionThe angles of a triangle are in the ratio 3:5:4. Find the measure of each of the angles.
View SolutionThe angles of a triangle are in the ratio 5:3:7, then the triangle is
View SolutionThe angles of a triangle are in the ratio 3:4:5. Find the smallest angle radian.
View Solution
