If the integers m and n are chosen at random between 1 and 100, then the probability that a number of the form 7m+7n is divisible by 5, equals (a) 14 (b) 17 (c) 18 (d) 149
14
12
18
13
The correct Answer is:A
Let l=7n+7m, then we observe that 71,72,73 and 74 ends in 7,9,3 and 1, respectively. Thus, 7i ends in 7,9,3 or 1 according as i is of the form 4k - 3, 4k - 2, 4k - 1 for 4k, respectively.
If S is the sample space, then n(S)=(100)2.
7m+7n is divisible by 5, if
(i) m is of the form 4k - 3 and n is of the form 4k - 1 for
(ii) m is of the form 4k - 2 and n is of the form 4k or
(iii) m is of the form 4k - 1 and n is of the form 4k - 3 or
(iv) m is of the form 4k and n is of the form 4k - 2.
Thus, number of favourable ordered pairs
(m,n)=4×25×25
∴ Required probability =4×25×25(100)2=14
Topper's Solved these Questions
- PROBABILITYBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:PROBABILITYExercise:PRACTICE EXERCISE (Exercies 2 (MISCELLANEOUS PROBLEMS))
Explore 30 Videos
- PROBABILITYBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:PROBABILITYExercise:Exercise 1 (TOPICAL PROBLEMS)
Explore 44 Videos
- PRACTICE SET 24Book:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:PRACTICE SET 24Exercise:Paper 2 (Mathmatics)
Explore 50 Videos
- SEQUENCES AND SERIES Book:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:SEQUENCES AND SERIES Exercise:EXERCISE 31
Explore 1 Video
Similar Questions
Two dice are thrown simultaneously. the probability of obtaining a total score of 5 is a. 1/18 b. 1/12 c. 1/9 d. none of these
View SolutionThe probability distribution of a random variable X is given as
Then, the value of p is

View SolutionThe switching function for the following network is
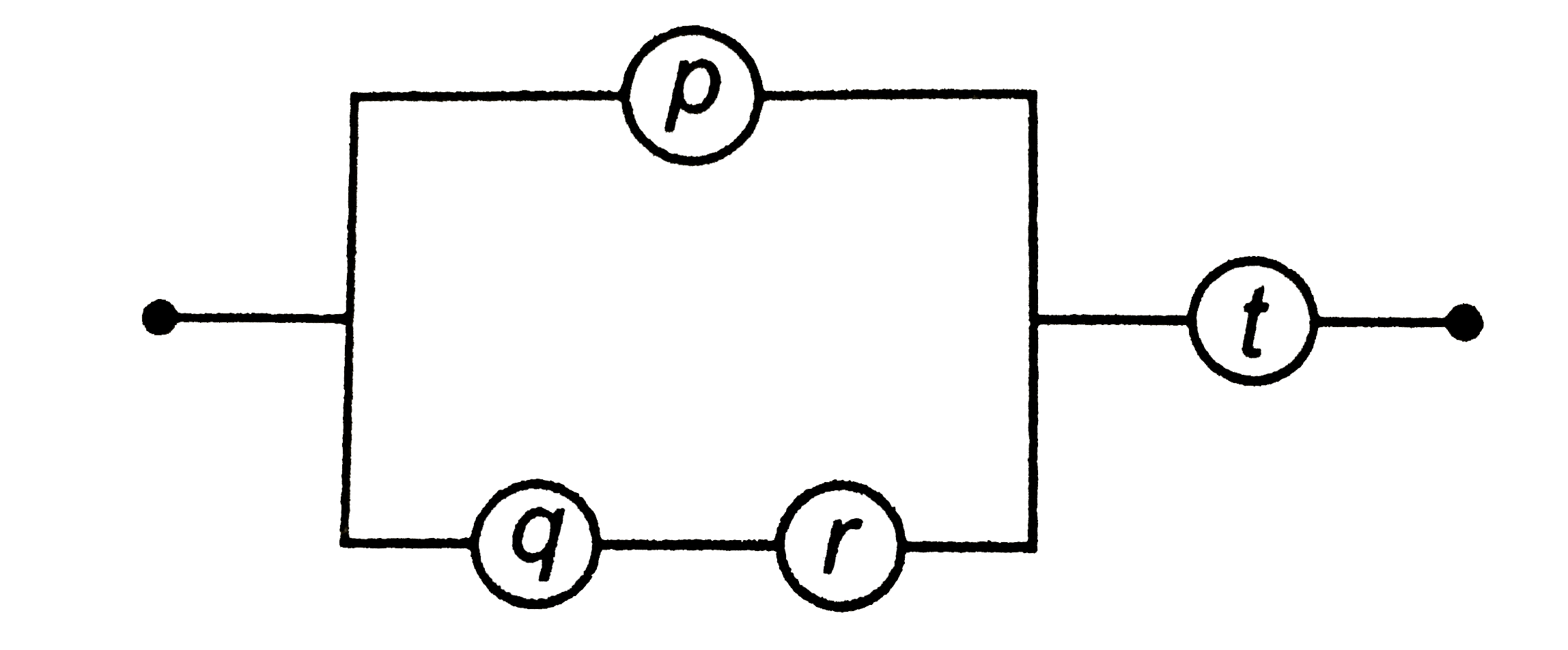
View SolutionThe coefficient of x3 in the expansion of 3x is
View SolutionIf the integers m and n are chosen at random between 1 and 100, then the probability that a number of the form 7m+7n is divisible by 5, equals (a) 14 (b) 17 (c) 18 (d) 149
View SolutionIf the integers m and n are chosen at random between 1 and 100, then the probability that a number of the form 7m+7n is divisible by 5, equals :
View Solutionयदि पूर्णांक m और n को यादृच्छिक रूप से (At random) 1 और 100 के बीच से चुना जाता है, तो संख्या 7m+7n के 5 से विभाजित होने की प्रायिकता है
View SolutionIf the integers m and n are chosen at random between 1 and 100, then atmost distinct numbers of the form 7m+7n is divisible by 5 equals to :
View Solutionlimn→∞1+15+125+.....+15n1+17+149+.....+17n =
View Solutionlimn→∞⎛⎝1+15+125±−−−+15n1+17+149±−−+17n⎞⎠=
View SolutionIf a positive integer is chosen at random, it is divisible by 7. What is the probability that the remainder is (i) 1, (ii) not 1.
View Solutionयदि पूर्णाक m और n को यादृच्छिक रूप से (At random) 1 और 100 के बीच से चुना जाता है, तो संख्या 7m+7n के 5 से विभाजित होने की प्रायिकता है
View SolutionIf the integers m and n are chosen at random between 1 and 100, then the probability that a number of the form 7m+7n is divisible by 5, equals (a) 14 (b) 17 (c) 18 (d) 149
View SolutionA number x is chosen at random from the numbers −3, −2, −1, 0, 1, 2, 3 the probability that |x|<2 is 57 (b) 27 (c) 37 (d) 17
View SolutionIf integers m and n are chosen randomly from 1 to 100, then the number 7^(m)+7^(n) The probability of dividing by 5 is
View SolutionA) 49n+16n+1 is divisible by A(n∈N)
B) 32n+7 is divisible by B(n∈N)
C) 4n−3n−1 is divisible by C(n∈n)
D) 33n−26n−1 is divisible by D(n∈N)
then the increasing order of A, B, C, D is
View Solution
