If the perimeter of the triangle formed by feet of altitudes of the triangle ABC is equal to four times the circumradius of ΔABC, then identify the type of ΔABCSolution in Bengali
The correct Answer is:Triangle is not possible
AD, BE and CF are altitudes.

DE=ccosC,EF=acosA,FD=bcosB
Given that 4R=acosA+bcosB+ccosC
⇒4R=R(sin2A+sin2B+sin2C)
⇒sinAsinBsinC=1
This is possible only when ∠A=∠B=∠C=π/2
So, triangle is not possible
टॉपर्स ने हल किए ये सवाल
- PROPERTIES AND SOLUTIONS OF TRIANGLEBook:CENGAGE PUBLICATIONChapter:PROPERTIES AND SOLUTIONS OF TRIANGLEExercise:Concept application exercise 5.10
Explore 8 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBook:CENGAGE PUBLICATIONChapter:PROPERTIES AND SOLUTIONS OF TRIANGLEExercise:Concept application exercise 5.11
Explore 4 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBook:CENGAGE PUBLICATIONChapter:PROPERTIES AND SOLUTIONS OF TRIANGLEExercise:Concept application exercise 5.8
Explore 7 Videos
- PROGRESSION AND SERIESBook:CENGAGE PUBLICATIONChapter:PROGRESSION AND SERIESExercise:ARCHIVES (NUMERICAL VALUE TYPE )
Explore 8 Videos
- RELATIONS AND FUNCTIONSBook:CENGAGE PUBLICATIONChapter:RELATIONS AND FUNCTIONSExercise:All Questions
Explore 1119 Videos
समान प्रश्न
In ΔABC, if r1<r2<r3, then find the order of lengths of the sides
View SolutionRegular pentagons are inscribed in two circles of radius 5and 2 units respectively. The ratio of their areas is
View SolutionIf the incircle of the triangle ABC passes through its circumcenter, then find the value of 4sin.A2sin.B2sin.C2
View SolutionLet Sk,k=1,2,….100 denote the sum of the infinite geometric series whose first term is k−1K! and the common
ration is 1k then the value of (100)2100!+Σ100k=1|(k^2-3k+1)S_k| is ____________
View SolutionIf the function f:[1,∞)→[1,∞) is defined by f(x)=2x(x−1), then find f−1(x)
View SolutionIn ΔABC if AD is the altitude and O is the orthocentre of ΔABC then AO:OD=
View SolutionIf in a ΔABC,AD,BEandCF are the altitudes and R is the circumradius, then find the radius of the DEF.
View SolutionIn a ΔABC,2s= perimeter and R = circumradius. Then, find sR.
View SolutionIn ΔABC,ifa=5,A=30∘, then the circumradius is
View SolutionBE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
View SolutionBE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
View SolutionABC is a triangle in which altitudes BE and CF to sides AC and AB are equal. Also ΔABE≅ΔACF.
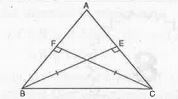 Then triangle ABC is :
Then triangle ABC is :
View SolutionLet D, E and F be the feet of altitudes from the vertices of acute -angled triangle ABC to the sides BC, AC and AB respectively. Triangle DEF is defined as the pedal triangle ABC. (R and rare circumradius and inradius of triangle of trangle ABC, respectivley)
Circumradius of a pedal triangle of triangle ABC is
View SolutionStatement. 1: The incenter of triangle ABC is the orthocenter of the triangle l1l2l3 where l1l2l3 are excenters of triangle ABC
Statement - 2: The incenter of the triangle formed by the feet of altitudes from the vertices of triangle ABC to the opposite sides is the orthocenter of the triangle ABC
View SolutionIn figure the perimeter of △ABC is
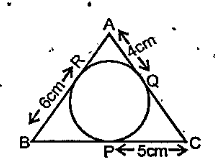
View SolutionABC is an equilateral triangle with side 10 cm. The perimeter of the triangle formed by joining the midpoints of the sides of Delta ABC is
View Solution
