If the roots of the equation (a2−bc)x2+2(b2−ac)x+(c2−ab)=0 are equal, where b≠0, then find the relation between a, b and c.
The correct Answer is:3abc
Topper's Solved these Questions
- SAMPLE PAPER 6BOOK - OSWAL PUBLICATIONCHAPTER - SAMPLE PAPER 6EXERCISE - Section - B
5 Videos
- SAMPLE PAPER 6BOOK - OSWAL PUBLICATIONCHAPTER - SAMPLE PAPER 6EXERCISE - Section -C
7 Videos
- SAMPLE PAPER 6BOOK - OSWAL PUBLICATIONCHAPTER - SAMPLE PAPER 6EXERCISE - Section -C
7 Videos
- SAMPLE PAPER 5BOOK - OSWAL PUBLICATIONCHAPTER - SAMPLE PAPER 5EXERCISE - Section -C
2 Videos
- SAMPLE PAPER 7BOOK - OSWAL PUBLICATIONCHAPTER - SAMPLE PAPER 7EXERCISE - Section -C
7 Videos
Similar Questions
Draw a circle of radius 4 cm. Draw two tangents to the circle inclined at an angle of 60∘ to each other.
View SolutionIn the given figure, a circle is inscribed in a quadrilateral ABCD in which ∠B=90∘. If AD = 23 cm, AB = 29 cm and DS = 5 cm, find the value of radius (r).
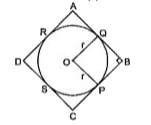
View SolutionIn the given figure, a circle is inscribed in a quadrilateral ABCD in which ∠B=90∘. If AD = 23 cm, AB = 29 cm and DS = 5 cm, find the value of radius (r).

View SolutionIf Sn denotes the sum of the first n terms of an A.P., prove that S30=3(S20−S10)
View SolutionA solid cylinder of diameter 12 cm and height 15 cm is melted and recast into 12 toys in the shape of a right-circular cone mounted on a hemisphere. Find the radius of the hemisphere if the height of the cone is 3 times the radius.
View SolutionThe condition for the roots of the equation,(c^(2)-ab)x^(2)-2(a^(2)-bc)x+(b^(2)-ac)=0 to be equal is:
View Solutionयदि समीकरण (c2−ab)x2−2(a2−bc)x+b2−ac=0 के मूल बराबर हैं, तो सिद्ध कीजिए की
a=0 या a3+b2+c3=3abc
View SolutionShow that the roots of the equation (a2−bc)x2+2(b2−ac)x+c2−ab=0
are equal if either b=0 or a3+b3+c3−3acb=0
View SolutionIf c2≠ab and the roots of (c2−ab)x2−2(a2−bc)x+(b2−ac)=0 are equal, then show that a3+b3+c3=3abc or a=0
View SolutionLet Δ=∣∣ ∣ ∣∣−bcb2+bcc2+bca2+ac−acc2+aca2+abb2+ab−ab∣∣ ∣ ∣∣ and the equation
x3−px2+qx−r=0 has roots a,b,c, where a,b,c ∈R+
The value of D≤ta is
View SolutionLet Δ=∣∣ ∣ ∣∣−bcb2+bcc2+bca2+ac−acc2+aca2+abb2+ab−ab∣∣ ∣ ∣∣ and the equation
x3−px2+qx−r=0 has roots a,b,c, where a,b,c ∈R+
If a,b,c are in GP then
View SolutionFind the product ⎡⎢⎣0c−b−c0an−a0⎤⎥⎦⎡⎢⎣a2abacabb2bcacbcc2⎤⎥⎦
View SolutionIf A=⎡⎢⎣a2abacabb2bcacbcc2⎤⎥⎦,B=⎡⎢⎣0c−b−c0ab−a0⎤⎥⎦ then AB=
View SolutionIf c2≠ab and the roots of (c2−ab)x2−2(a2−bc)x+(b2−ac)+0 are equal show that a3+b3+c3=3abc (or) a = 0.
View SolutionIf the roots of the equation (c2−ab)x2−2(a2−bc)x+b2−ac=0 in x are equal, show that either a=0 or a3+b3+c3=3abc.
View SolutionShow that the roots of the equation (a2−bc)x2+2(b2−ac)x+c2−ab=0
are equal if either b=0 or a3+b3+c3−3acb=0
View Solution
