If the sum of any pair of opposite angles of a quadrilateral is 180∘; then the quadrilateral is cyclic.
Let ABCD be a cyclic quadrilateral.
Let us join OB and OD.
Then, ∠BOD=2∠BCD
∠BCD=12∠BOD
Similarly, ∠BAD=12∠DOB
∴∠BAD+∠BCD=12∠BOD+12+∠DOB
=12(∠BOD+∠DOB)=12×360∘
=180∘
Similarly, ∠B+∠D=180∘
Topper's Solved these Questions
Similar Questions
In ABC,D is the mid-point of AB,P is any point of BC.CQPD meets AB in Q . Show that ar(BPQ)=12ar(ABC). TO PROVE : ar(BPQ)=12ar(ABC) CONSTRUCTION : Join CD.
View SolutionIn Figure, AB=AC.BE and CF are respectively the bisectors of ∠B and ∠C . Prove that EBC=FCB. Figure
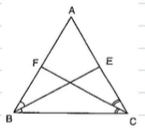
View SolutionProve that the sum of opposite pair of angles of a cyclic quadrilateral is 180^(@)
View SolutionThe sum of either pair of opposite angles of a cyclic quadrilateral is 1800 OR The opposite angles of a cyclic quadrilateral are supplementary.
View SolutionIf the sum of any pair of opposite angles of a quadrilateral is 180∘; then the quadrilateral is cyclic.
View SolutionTheorem 10.12 : If the sum of a pair of opposite angles of a quadrilateral is 180º, the quadrilateral is cyclic.
View Solutionसिद्ध कीजिए की चक्रीय चतुर्भुज के सम्मुख कोण युग्म संपूण्क या उनका योग 180∘ होगा है
View Solutionसिद्ध कीजिए कि किसी चतुर्भुज के किसी भी युग्म का योगफल 180∘ हो तो चतुर्भुज चक्रीय होता है।
View SolutionIf the degree measure of the sum of any two opposite angles of a quadrilateral is ………….. ,then it is a cyclic quadrilateral.
View SolutionSum of opposite angles in a cyclic quadrilateral is …………
View SolutionThe sum of either pair of opposite angles of a cyclic quadrilateral is
View SolutionThe sum of either pair of opposite angles of a cyclic quadrilateral is
View Solutionಒಂದು ಚಕ್ರೀಯ ಚತುರ್ಭುಜದ ಅಭಿಮುಖ ಕೋನಗಳ ಮೊತ್ತ
View Solutionकिसी चक्रीय चतुर्भुज के सम्मुख कोणों का योग होता है -
View SolutionProve that the sum of opposite pair of angles of a cyclic quadrilateral is 180∘
View SolutionThe sum of either pair of opposite angles of a cyclic quadrilateral is 1800 OR The opposite angles of a cyclic quadrilateral are supplementary.
View Solution