If x:a=y:b=z:c, then prove that
x3a2+y3b2+z3c2=(x+y+z)3(a+b+c)2Solution in Bengali
Given that x:a=y:b=z:c
or, xa=yb=zc=k(k≠0)(let)
∴X=ak,y=bk,z=ck.
LHS =x3a2+y3b2+z3c2=(ak)3a2+(bk)3b2+(ck)3c2
=a3k3a2+b3k3b2+c3k3c2=ak3+bk3+ck3
=k3(a+b+c).
RHS =(x+y+z)3(a+b+c)2=(ak+bk+ck)3(a+b+c)2
={k(a+b+c)}3(a+b+c)2=k3(a+b+c)3(a+b+c)2=k3(a+b+c).
∴ LHS = RHS
Similar Questions
Prove that ∣∣ ∣ ∣∣ax−by−czay+bxcx+azay+bxby−cz−axbz+cycx+azbz+cycz−ax−by∣∣ ∣ ∣∣=(x2+y2+z2)(a2+b2+c2)(ax+by+cz).
View SolutionProve that |ax−by−czay+bxcx+azay+bxby−cz−axbz+cycx+azbz+cycz−ax−by|=(x2+y2+z2)(a2+b2+c2)(ax+by+cz).
View Solutionयदि xa=yb=zc, सिद्ध करे की
x3a2+y3b2+z3c2=(x+y+z)3(a+b+c)2
View SolutionIf (x)/(a) = (y)/(b) = (z)/(c ) , Prove that ((a^(2)x^(2)+b^(2)y^(2)+c^(2)z_(2))/(a^(3)x+b^(3)ty+c^(3)z))=(xyz)/(abc)
View SolutionSuppose a, b and c are distinct and x,y and z are connected by the system of eqations x+ay+a2z=a3,x+by+b2z=b3andx+cy+c2z=c3.
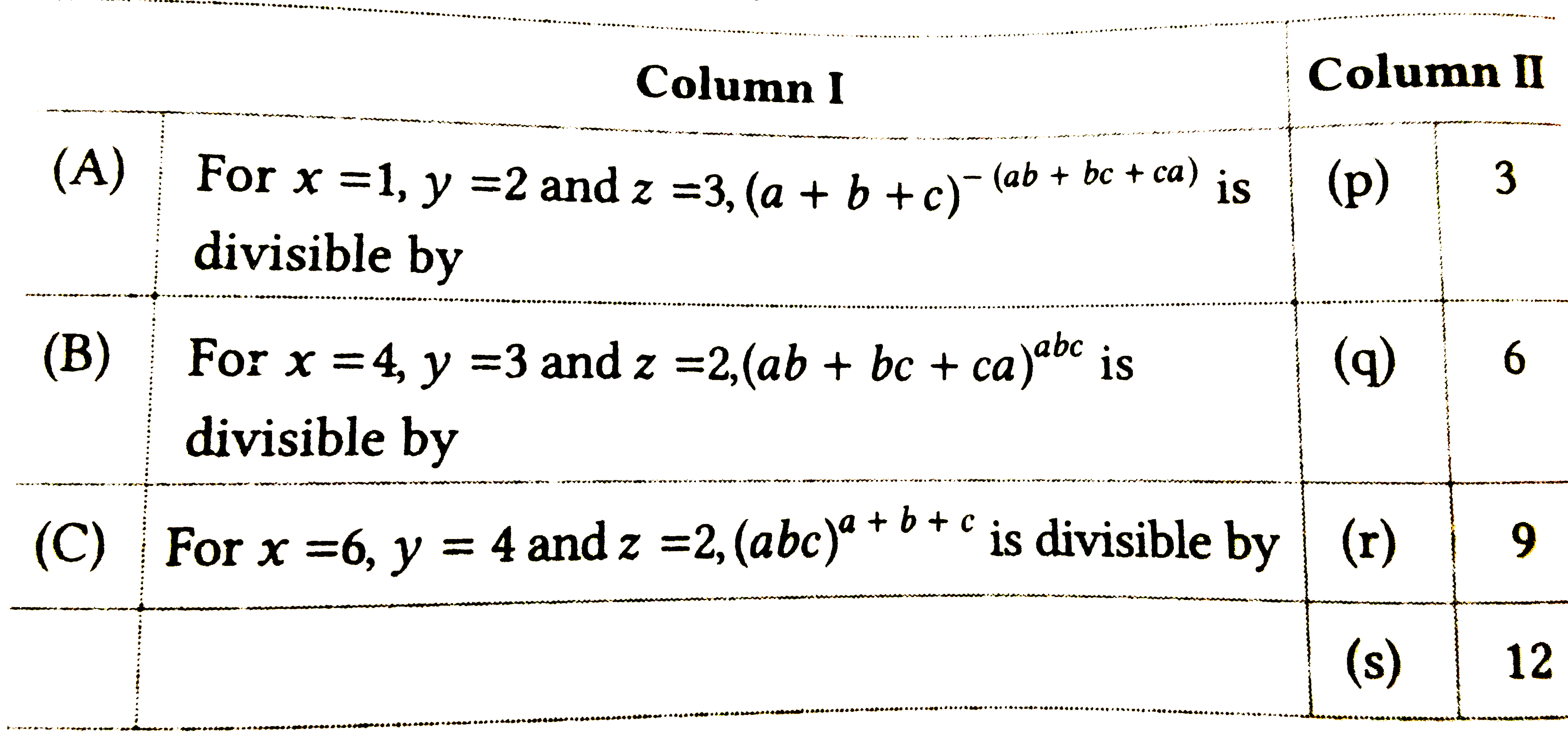
View SolutionIf xa=yb=zc, then show that x3+a3x2+a2+y3+b3y2+b2+z3+c3z2+c2=(x+y+z)3+(a+b+c)2(x+y+z)2+(a+b+c)2.
View SolutionProve that |a x-b y-c z a y+b x c x+a z a y+b x b y-c z-a x b z+c y c x+a z b z+c y c z-a x-b y|=(x^2+y^2+z^2)(a^2+b^2+c^2)(a x+b y+c z)dot
View SolutionUsing the properties of determinants prove that |{:(a+b+2c,a,b),(c,b+c+2a,b),(c,a,c+a+2b):}|=2(a+b+c)^3 or |{:(x+y+2z,x,y),(z,y+z+2x,y),(z,x,z+x+2y):}|=2(x+y+z)^3
View Solution
