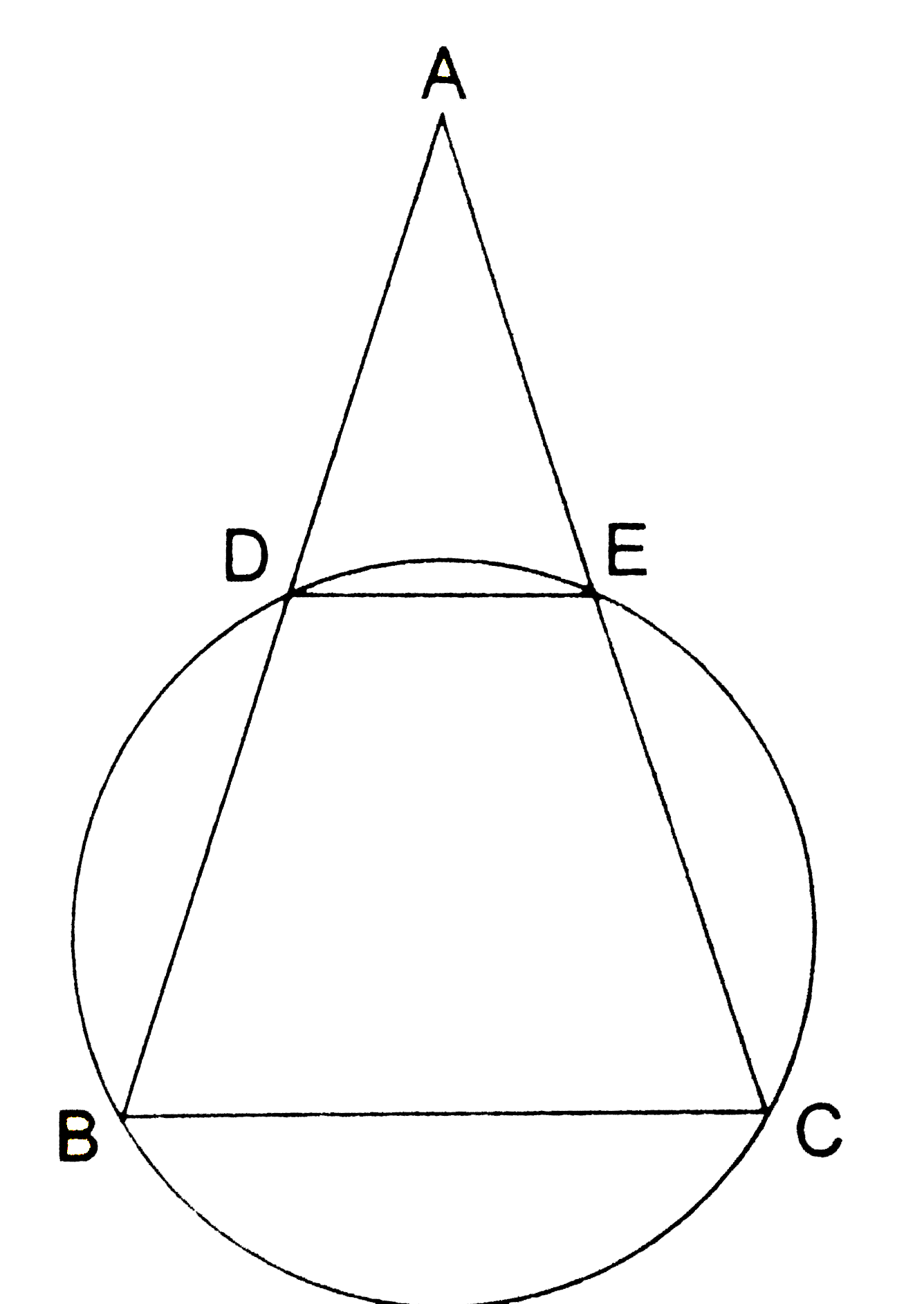
In an isosceles triangle ABC with AB=AC, a circle passing through B and C intersects the sides AB and AC at D and E respectively. Prove that DEBC
AB= AC
⇒∠ABC=∠ACB ….(i)
Side BD of the cyclic quadrilateral BCED is produced to A.
∴∠ADE=∠ACB …(ii)
[ext. ∠ADE=int. opp. ∠C] .
From (i) and (ii) , we get
∠ABC=∠ADE.
But, these are corresponding angles.
Hence,DE∣∣BC
Similar Questions
AD and BE are respectively altitudes of ABC such that AE=BD. Prove that AD=BE.
View SolutionIn Figure, AD and BE are respectively altitudes of an isosceles triangle ABC with AC=BC. Prove that AE=BD
View SolutionABC and DBC are two isosceles triangles on the same bas BC and vertices A and D are on the same side of BC . If AD is extended to intersect BC at P, show that ABD ≅ACD (ii) ABP ≅ACP
View SolutionAD, BE and CF, the altitudes of ABC are equal. Prove that ABC is an equilateral triangle.
View SolutionFill in the blanks in the following so that each of the following statements is true.
(i) Sides opposite to equal angles of a triangle are .......
(ii) Angle opposite to equal sides of a triangle are .......
(iii) In an equilateral triangle all angles are .......
(iv) In a ABC if ∠A=∠C, then AB= .....
(v) If altitudes CE and BF of a triangle ABC are equal, then AB= ........
(vi) In an isosceles triangle ABC with AB=AC, if BD and CE are its altitudes, then BD is .......... CE.
(vii) In right triangles ABC and DEF, if hypotenuse AB=EF and side AC=DE, then ABC ≅ ....
View SolutionD, E, F are the mid-point of the sides BC, CA and AB respectively of △ABC. Then DEF is congruent to triangle.
(a)ABC
(b) AEF
(c) BFD, CDE
(d) AFE, BFD, CDE
View SolutionIn Figure, AB and AC are two equal chords of a circle whose centre is O. If OD ⊥AB and OE ⊥AC, prove that △ADE is an isosceles triangle.
View SolutionIn Figure, AB=CD. Prove that BE=DE and AE=CE, where E is the point of intersecting of AD and BC.
View Solution
