In ΔABC, tan B =√3 , find the values of cosec B and cos B.
Video Solution
Text Solution
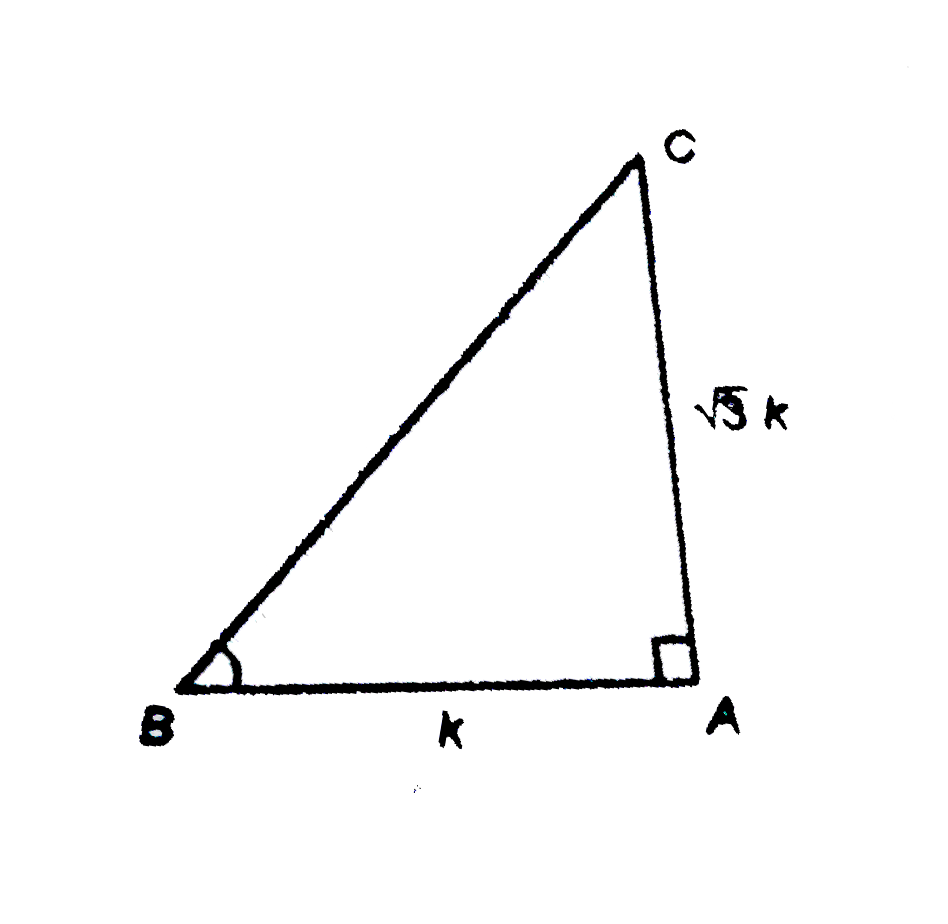
Construct a right - angled triangle ABC in which tanB=√3=√31=perpendicularbase=ACAB
Let AC=√3kandAB=k
From Pythagoras theorem
BC2=AB2+AC2
=(k)2+(√3k)2
BC2=k2+3k2=4k2
⇒ BC=2k
∴ cosecB=hypotenuseperpendicular=BCAC=2k√3k=2√3
and cosB=basehypotenuse=ABBC=k2k=12
|
Topper's Solved these Questions
- INTRODUCTION TO TRIGONOMETRYBook:NAGEEN PRAKASHAN ENGLISHChapter:INTRODUCTION TO TRIGONOMETRYExercise:Problems From NCERT/exemplar
Explore 29 Videos
- INTRODUCTION TO TRIGONOMETRYBook:NAGEEN PRAKASHAN ENGLISHChapter:INTRODUCTION TO TRIGONOMETRYExercise:Exercise 8a
Explore 20 Videos
- CONSTRUCTIONSBook:NAGEEN PRAKASHAN ENGLISHChapter:CONSTRUCTIONSExercise:Exercise 11 B
Explore 10 Videos
- LINEAR EQUATIONS IN TWO VARIABLES Book:NAGEEN PRAKASHAN ENGLISHChapter:LINEAR EQUATIONS IN TWO VARIABLES Exercise:Revision Exercise Long Answer Questions
Explore 8 Videos
Similar Questions
Knowledge Check
In △ABC, a = 2, b = 3,c = 4 , then the value of cos A is
A2124B2112C2421D2412
Let A,B,C be the three angles such that A+B+C=π,tanA.tanB=2, then find the value of cosAcosBcosC
View SolutionIn ΔABC a =5 ,b=3 ,c=7 .Then value of 3cosC+7cosB is equal :-
View SolutionIf tan A =1 and tan b = √3 , evaluate :
sin A cos B+ cos A sin B.
View SolutionA triangle ABC is right angled at B, find the value of
secA.cosecC−tanA.cotCsinB
View SolutionIf tan A =1 and tan b = √3 , evaluate :
cos A cos B - sin A sin B.
View SolutionIn triangle ABC, right-angled at B. if tanA=1√3find the value of:
(i) sinAcosC+cosAsinC
(ii) cosAcosCsinAsinC
View SolutionIn triangle ABC,∠C=2π3 then the value of cos2A+cos2B−cosA.cosB is equal
View Solution