In ΔABCand ΔDEF, AB = DE, AB ∣∣ DE, BC = EF and BC ∣∣ EF. Vertices A, B and C are joined to vertices D, E and F respectively (see Fig. 8.22).Show that
(i) quadrilateral ABED is a parallelogram
(ii) quadrilateral BEFC is a parallelogram
(iii) AD || CF and AD = CF
(iv) quadrilateral ACFD is a parallelogram
(v) AC = DF
(vi) ∆ ABC ≅ ∆ DEF.
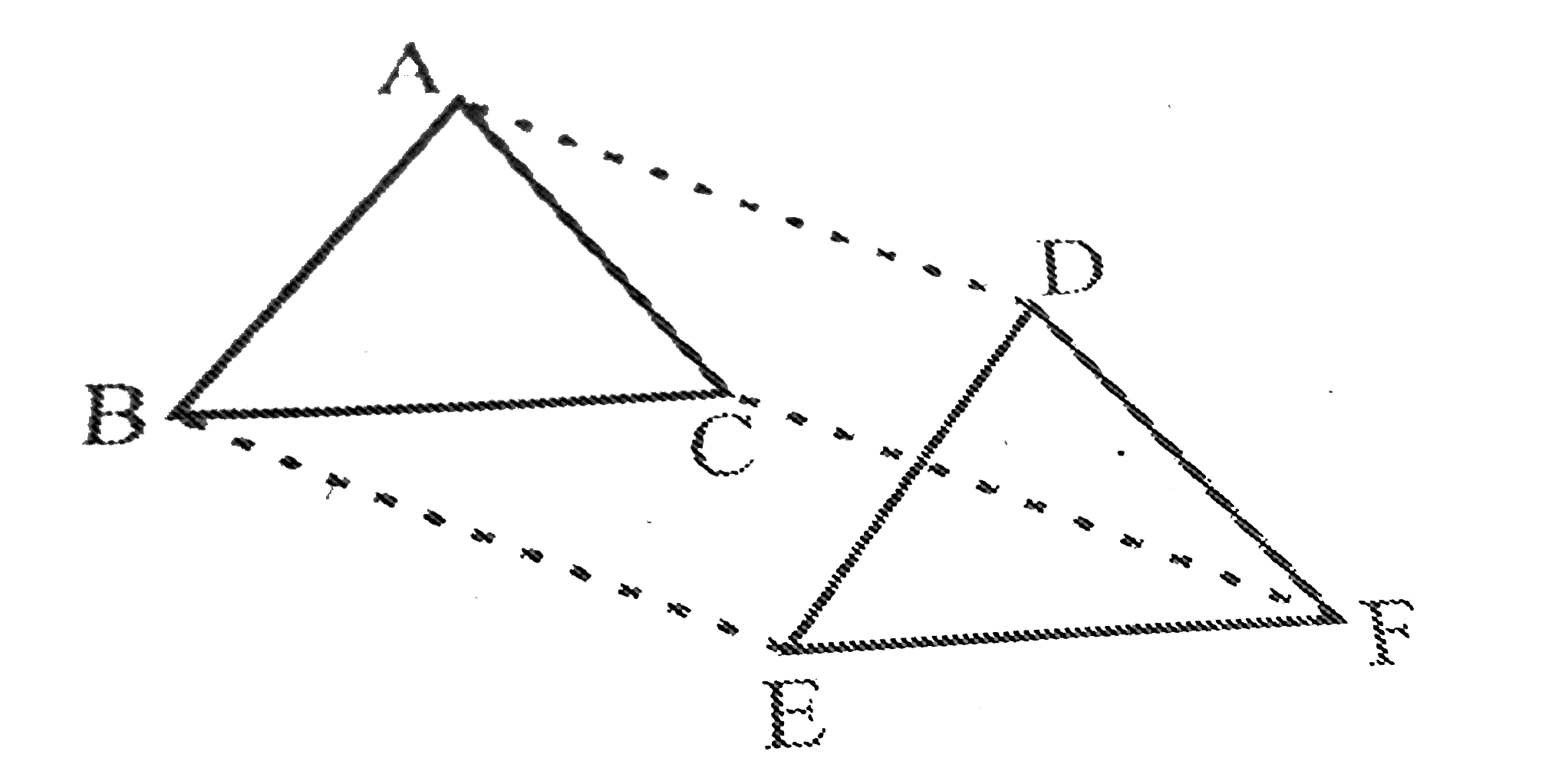
(i) Given, AB = DE and AB ||DE
If one pair of opposite sides of a quadrilateral are equal and parallel to each other,
then it is a parallelogram.
Thus, quadrilateral ABED is a parallelogram.
(ii)Again, BC = EF and BC || EF
Therefore, quadrilateral BEFC is a parallelogram using the concept discussed in (i).
(iii) As ABED and BEFC are parallelograms,
So,AD = BE and AD || BE
and ,BE = CF and BE || CF
(Opposite sides of a parallelogram are equal and parallel)
Therefore, AD = BE = CF and AD || BE || CF
(iv) As we observed that AD and CF are equal
and parallel to each other, therefore, it is a parallelogram.
(v) As ACFD is a parallelogram,
therefore, the pair of opposite sides will be equal and parallel to each other
∴ AC || DF and AC = DF
(vi) ∆ABC and ∆DEF,
=>BC = EF
=>AB = DE
=>AC = DF (Since ACFD is a parallelogram)
∴ ∆ABC ≅ ∆DEF (By SSS congruence rule)
Similar Questions
If ABC and DEF are two triangles such that AB, BC are respectively equal and parallel to DE, EF, then show that Quadrilateral ABED is a parallelogram Quadrilateral BCFE is a parallelogram AC=DF (iv) ABC ≅ DEF
View SolutionIn an equilateral triangle ABC, D, E, F are the mid-points of AB, BC and AC respectively.The quadrilateral BEFD is are a
(A) Square
(B) Parallelogram
(C) Rectangle
(D) Rhombus
View SolutionPoint E and F lie on diagonals AC of a parallelogram ABCD such that AnE=CF. What type of quadrilateral is BFDE? From the given figure we see that BFDEis also a parallelogram.
View SolutionD, E and F are respectively the mid-points of the sides BC, CA and AB of aΔABC.Show that (i) BDEF is a parallelogram. (ii) ar (DEF)=14ar (ABC)(iii) ar (BDEF)=12ar (ABC)
View SolutionIn Fig. 7.21, AC = AE, AB = ADand ∠BAD =∠EAC. Show that BC = DE.
View SolutionIn a parallelogram ABCD,E,F are any two points on the sides AB and BC respectively. Show that ar(ADF)=ar(DCE).
View SolutionThe sides AB and CD of a parallelogram ABCD are bisected at E and F. Prove that EBFD is a parallelogram.
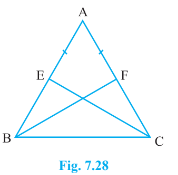
View SolutionE and F are respectively the mid-points of equal sides AB and AC of ΔABC(see Fig. 7.28). Show that BF = C E.
View SolutionABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see Fig. 7.32). Show that
(i) ΔABE≅ΔACF
(ii) AB = AC, i.e., ABC is an isosceles triangle.
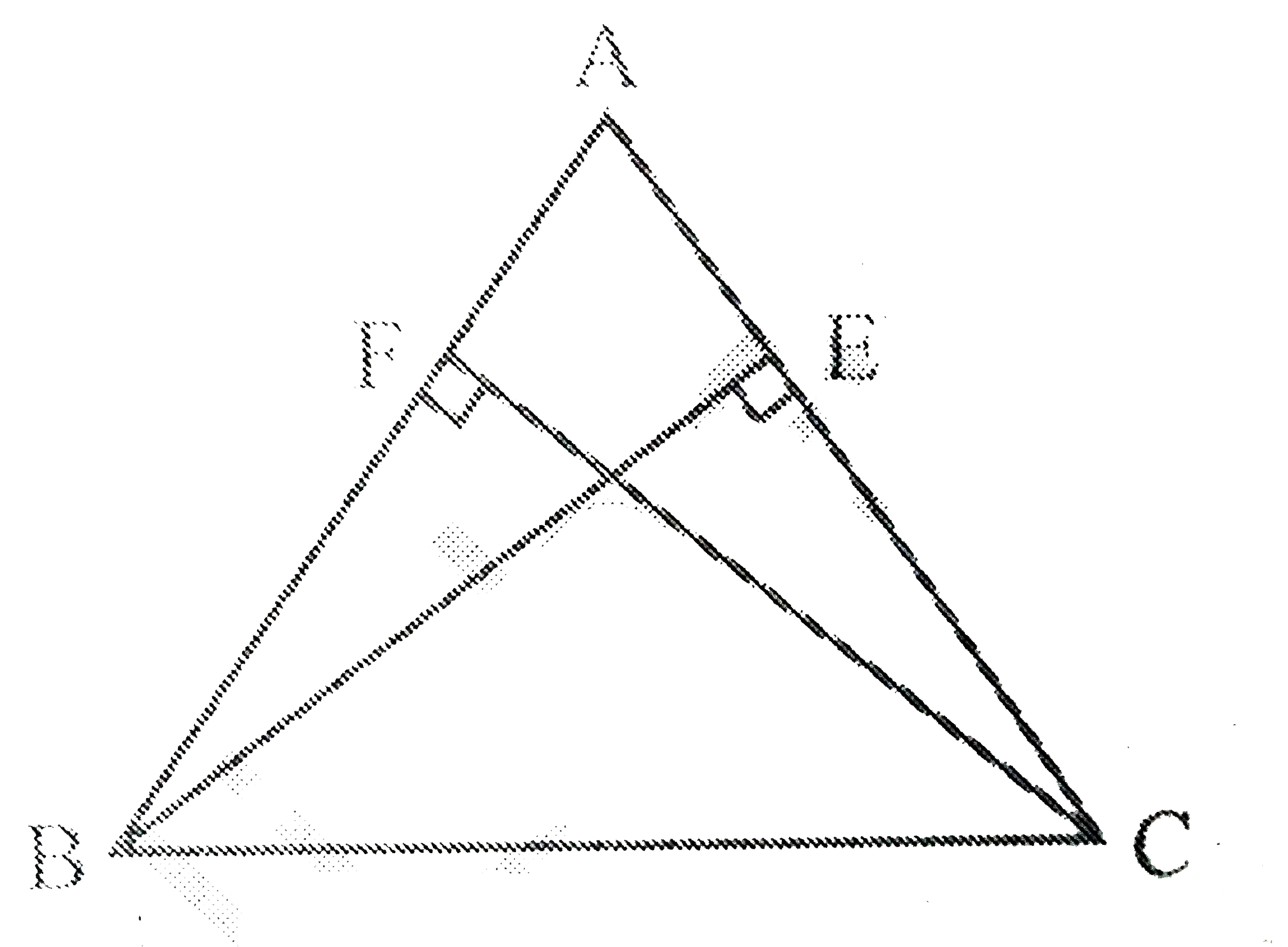
View SolutionIn quadrilateral ACBD, AC = ADand AB bisects ∠A(see Fig. 7.16). Show that ΔABC≅ΔABD

View Solution