In ΔABCand ΔDEF, AB = DE, AB ∣∣ DE, BC = EF and BC ∣∣ EF. Vertices A, B and C are joined to vertices D, E and F respectively (see Fig. 8.22).Show that (i) quadrilateral ABED is a parall
Step by step video solution for In DeltaA B Cand DeltaD E F, A B\ =\ D E, A B\ ||\ D E, B C\ =\ E F and B C\ ||\ E F. Vertices A, B and C are joined to vertices D, E and F respectively (see Fig. 8.22).Show that (i) quadrilateral ABED is a parall by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUADRILATERALS Book:MTG IIT JEE FOUNDATIONChapter:QUADRILATERALS Exercise:NCERT SECTION (Exercise 8.2 )
Explore 11 Videos
- QUADRILATERALS Book:MTG IIT JEE FOUNDATIONChapter:QUADRILATERALS Exercise:EXERCISE (Multiple Choice Questions) (LEVEL-1 )
Explore 35 Videos
- QUADRILATERALS Book:MTG IIT JEE FOUNDATIONChapter:QUADRILATERALS Exercise:SOLVED EXAMPLES
Explore 12 Videos
- PROBABILITYBook:MTG IIT JEE FOUNDATIONChapter:PROBABILITYExercise:OLYMPIAD/HOTS CORNER
Explore 20 Videos
- STATISTICSBook:MTG IIT JEE FOUNDATIONChapter:STATISTICSExercise:Olympiad/HOTS Corner
Explore 20 Videos
Similar Questions
Most A, B, C, D, E and F refer to

View SolutionIn Fig. 7.21, AC = AE, AB = ADand ∠BAD =∠EAC. Show that BC = DE.
View SolutionIn a parallelogram ABCD,E,F are any two points on the sides AB and BC respectively. Show that ar(ADF)=ar(DCE).
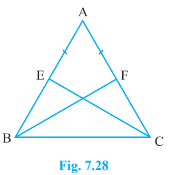
View SolutionE and F are respectively the mid-points of equal sides AB and AC of ΔABC(see Fig. 7.28). Show that BF = C E.
View SolutionXY isa line parallel to side BC of ABC.BEA and CFAB meet XY in E and F respectively.Show that ar(ABE)=ar(ACF).
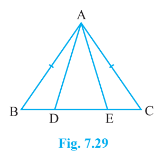
View SolutionIn an isosceles triangle ABC with AB=AC, D and E are points on BCsuch that BE=CD(see Fig. 7.29). Show that AD=AE
View SolutionIn figure, if ΔABE≅ΔACD, show that ΔADE~ΔABC.

View SolutionIn Fig. 71, if ABCD and CDEF, find ∠ACE
View SolutionABCD is a square E, F, G and H are points on AB, BC, CD and DA respectively, such that AE=BF=CG=DH. Prove that EFGH is square.
View SolutionABCD is a parallelogram and EandF are the centroids of triangles ABD and BCD respectively, then EF= (a)AE (b) BE (c) CE (d)DE
View Solution